题目内容
在△ABC中,角A,B,C的对边分别是a,b,c,并且满足acosB=bcosA,那么△ABC的形状为 .
考点:正弦定理
专题:解三角形
分析:由已知条件acosB=bcosA,利用余弦定理得到a
=b
,解得a=b.从而判定△ABC为等腰三角形.
| a2+c2-b2 |
| 2ac |
| b2+c2-a2 |
| 2bc |
解答:
解:∵acosB=bcosA
由余弦定理知,
cosB=
,cosA=
∴a
=b
化简得a2=b2
∴a=b
∴△ABC为等腰三角形
解法二:
acosB=bcosA
⇒sinAcosB-sinBcosA=0
⇒sin(A-B)=0
∵A,B为三角形的内角
故A=B
∴△ABC为等腰三角形
由余弦定理知,
cosB=
| a2+c2-b2 |
| 2ac |
| b2+c2-a2 |
| 2bc |
∴a
| a2+c2-b2 |
| 2ac |
| b2+c2-a2 |
| 2bc |
化简得a2=b2
∴a=b
∴△ABC为等腰三角形
解法二:
acosB=bcosA
⇒sinAcosB-sinBcosA=0
⇒sin(A-B)=0
∵A,B为三角形的内角
故A=B
∴△ABC为等腰三角形
点评:本题考查利用余弦定理判定三角形的形状.考查学生对公式的掌握及应用.属于中档题.

练习册系列答案
相关题目
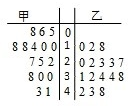 甲乙两组统计数据用茎叶图表示,设甲乙两组数据的平均数分别为
甲乙两组统计数据用茎叶图表示,设甲乙两组数据的平均数分别为. |
| x甲 |
. |
| x乙 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
sin(-585°)的值为( )
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|