题目内容
对于数列{an},定义Hn=
为{an}的“优值”,现在已知某数列{an}的“优值”Hn=2n+1,记数列{an-kn}的前n项和为Sn,若Sn≤S5对任意的n(n∈N*)恒成立,则实数k的取值范围为 .
| a1+2a2+…+2n-1an |
| n |
考点:数列与函数的综合
专题:计算题,等差数列与等比数列
分析:由题意,a1+2a2+…+2n-1an=n2n+1,a1+2a2+…+2n-2an-1=(n-1)2n,从而求出an=2(n+1),可得数列{an-kn}为等差数列,从而将Sn≤S5对任意的n(n∈N*)恒成立化为a5≥0,a6≤0;从而求解.
解答:
解:由题意,
Hn=
=2n+1,
则a1+2a2+…+2n-1an=n2n+1,
a1+2a2+…+2n-2an-1=(n-1)2n,
则2n-1an=n2n+1-(n-1)2n
=(n+1)2n,
则an=2(n+1),
对a1也成立,
故an=2(n+1),
则an-kn=(2-k)n+2,
则数列{an-kn}为等差数列,
故Sn≤S5对任意的n(n∈N*)恒成立可化为
a5≥0,a6≤0;
即
解得,
≤k≤
,
故答案为:
≤k≤
.
Hn=
| a1+2a2+…+2n-1an |
| n |
则a1+2a2+…+2n-1an=n2n+1,
a1+2a2+…+2n-2an-1=(n-1)2n,
则2n-1an=n2n+1-(n-1)2n
=(n+1)2n,
则an=2(n+1),
对a1也成立,
故an=2(n+1),
则an-kn=(2-k)n+2,
则数列{an-kn}为等差数列,
故Sn≤S5对任意的n(n∈N*)恒成立可化为
a5≥0,a6≤0;
即
|
解得,
| 7 |
| 3 |
| 12 |
| 5 |
故答案为:
| 7 |
| 3 |
| 12 |
| 5 |
点评:本题考查了等差数列的前n项和的最值及数列的通项公式的求法的问题,属于中档题.

练习册系列答案
相关题目
函数函数y=
的定义域是( )
| lg(3x+1) | ||
|
| A、∅ | ||
B、(-
| ||
C、(-
| ||
D、(-∞,-
|
如下图2,在平行四边形ABCD中,AD=2AB=2,∠BAC=90°.将△ACD沿AC折起,使得BD=
.在三棱锥D-ABC的四个面中,下列关于垂直关系的叙述错误的是( )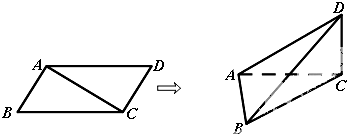
| 5 |

| A、面ABD⊥面BCD |
| B、面ABD⊥面ACD |
| C、面ABC⊥面ACD |
| D、面ABC⊥面BCD |
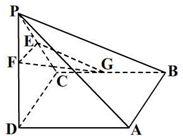 如图所示,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,点E,F,G分别为PC,PD,BC的中点.
如图所示,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,点E,F,G分别为PC,PD,BC的中点.