Question

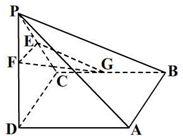如图所示，四棱锥P-ABCD中，底面ABCD为正方形，PD⊥平面ABCD，PD=AB=2，点E，F，G分别为PC，PD，BC的中点．
（Ⅰ）求证：PA∥平面EFG；
（Ⅱ）求三棱锥P-EFG的体积；
（Ⅲ）求四棱锥P-ABCD被平面EFG所截得到的两部分体积之比．

Answer 1

考点：棱柱、棱锥、棱台的体积,直线与平面平行的判定

专题：空间位置关系与距离,空间角

分析：（Ⅰ）首先利用题中的中点找到线线平行进一步利用线面平行的判定定理得出结论．
（Ⅱ）先证明GC⊥平面PCD，进一步转换∴VP-EFG=VG-PEF=

1

3

S△PEF．GC，利用相关的线段长求出体积．
（Ⅲ）利用割补法分别求出平面两边的体积，最后确定结果．

解答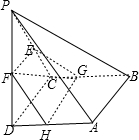： （Ⅰ）证明：如图，取AD的中点H，连接GH，FH，
∵E，F分别为PC，PD的中点，∴EF∥CD．
∵G，H分别为BC，AD的中点，
∴GH∥CD．∴EF∥GH．∴E，F，H，G四点共面．
∵F，H分别为DP，DA的中点，
∴PA∥FH．
∵PA不在平面EFG，FH?平面EFG，
∴PA∥平面EFG．
（II）解：∵PD⊥平面ABCD，GC?平面ABCD，
∴GC⊥PD．
∵ABCD为正方形，∴GC⊥CD．∵PD∩CD=D，
∴GC⊥平面PCD．
∵PF=

1

2

PD=1  EF=

1

2

CD=1，
∴S△PEF=

1

2

EF•PF=

1

2

．
∵GC=

1

2

BC=1，
∴VP-EFG=VG-PEF=

1

3

S△PEF•GC=

1

6

．
（Ⅲ）解：VP-ABCD=

1

3

AB•AD•PD=

8

3

，
采用割补法求被平面EFG所截得到下面的几何体的体积为：
V₁=V_DFH-GCE=

1

2

×DH×DF×GH-

1

3

×

1

2

×DH×DF×EF=

5

6

，
被平面EFG所截得到上面的几何体的体积为：V2=

8

3

-

5

6

=

11

6

，

V1

V2

=

5

11

．

点评：本题考查的知识要点：线面平行的判定定理，线面垂直的判定定理，锥体的体积公式的应用，割补法在几何题中的应用及相关的运算问题．属于基础题型．