题目内容
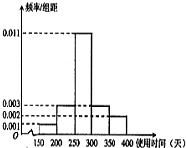 从某节能灯生产线上随机抽取100件产品进行寿命试验,按连续使用时间(单位:天)共分5组,得到频率分布直方图如图.
从某节能灯生产线上随机抽取100件产品进行寿命试验,按连续使用时间(单位:天)共分5组,得到频率分布直方图如图.(1)请根据频率分布直方图,估算样本数据的众数和中位数(中位数精确到0.01);
(2)若将频率视为概率,从该生产线所生产的产品(数量很多)中随机抽取3个,用ξ表示连续使用寿命高于350天的产品件数,求ξ的分布列和期望.
考点:离散型随机变量的期望与方差,频率分布直方图
专题:概率与统计
分析:(1)由频率分布直方图,得到众数落在第三组[250,300),由此能求出众数;数据落在第一、二组的频率是0.2<0.5,数据落在第一、二、三组的频率是0.75>0.5,所以中位数一定落在第三组[250,300)中,假设中位数是x,则0.2+(x-250)×0.011=0.5,由此能求出中位数.
(Ⅱ)由题意ξ=0,1,2,3,ξ~B(3,0.1),由此能求出ξ的分布列和期望.
(Ⅱ)由题意ξ=0,1,2,3,ξ~B(3,0.1),由此能求出ξ的分布列和期望.
解答:
解:(1)由频率分布直方图,得到众数落在第三组[250,300),
是
=275.(2分)
∵数据落在第一、二组的频率=50×0.001+50×0.003=0.2<0.5,(3分)
数据落在第一、二、三组的频率=50×0.001+50×0.003+50×0.011=0.75>0.5,
∴中位数一定落在第三组[250,300)中,(4分)
假设中位数是x,则0.2+(x-250)×0.011=0.5,
解得中位数x≈277.27.(5分)
(Ⅱ)∵样本中连续使用寿命高于350天的产品有10件,
所点频率为0.1,若将频率视为概率0.1,
依题意ξ=0,1,2,3,ξ~B(3,0.1),
P(ξ=0)=
×0.93=0.729,
P(ξ=1)=
×0.1×0.92=0.243,
P(ξ=2)=
×0.12×0.9=0.027,
P(ξ=3)=
0.13=0.001,(11分)
∴ξ的分布列为:
∴Eξ=np=3×0.1=0.3.(13分)
是
| 250+300 |
| 2 |
∵数据落在第一、二组的频率=50×0.001+50×0.003=0.2<0.5,(3分)
数据落在第一、二、三组的频率=50×0.001+50×0.003+50×0.011=0.75>0.5,
∴中位数一定落在第三组[250,300)中,(4分)
假设中位数是x,则0.2+(x-250)×0.011=0.5,
解得中位数x≈277.27.(5分)
(Ⅱ)∵样本中连续使用寿命高于350天的产品有10件,
所点频率为0.1,若将频率视为概率0.1,
依题意ξ=0,1,2,3,ξ~B(3,0.1),
P(ξ=0)=
| C | 0 3 |
P(ξ=1)=
| C | 1 3 |
P(ξ=2)=
| C | 2 3 |
P(ξ=3)=
| C | 3 3 |
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | 0.729 | 0.243 | 0.027 | 0.001 |
点评:本题考查众数、中位数的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
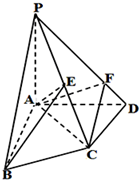 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC=3
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC=3