题目内容
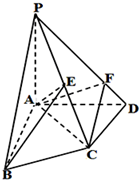 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC=3
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC=3| 3 |
(Ⅰ)求证:PD⊥面ABE;
(Ⅱ)在线段PD上存在点F,使得CF∥面PAB,试确定点F的位置,并求棱锥D-ACF的体积.
考点:直线与平面垂直的判定,平面与平面平行的判定,直线与平面垂直的性质
专题:综合题,空间位置关系与距离
分析:(Ⅰ)证明PD⊥面ABE,关键是证明AB⊥PD,AE⊥PD;
(Ⅱ)在底面ABCD中过点C作CM∥AB交AD与点M,在△PAD中过点M作MF∥PA交PD于点F,连接CF,利用面面平行,可得在线段PD上存在点F满足DF=
DP,使CF∥面PAB;利用VD-ACF=VF-ACD=
S△ACD•hF=
S△ACD•PA,可求棱锥D-ACF的体积.
(Ⅱ)在底面ABCD中过点C作CM∥AB交AD与点M,在△PAD中过点M作MF∥PA交PD于点F,连接CF,利用面面平行,可得在线段PD上存在点F满足DF=
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 12 |
解答:
 (Ⅰ)证明:∵PA⊥底面ABCD,
(Ⅰ)证明:∵PA⊥底面ABCD,
∴PA⊥AB,PA⊥CD
又AB⊥AD,∴AB⊥面PAD,∴AB⊥PD …(2分)
又AC⊥CD,∴CD⊥面PAC,∴CD⊥AE …(3分)
∵PA=AB=BC=AC,E是PC的中点,
∴AE⊥PC,
∵CD∩PC=C,
∴AE⊥面PCD,
∴AE⊥PD …(4分)
∵AB∩AE=A,
∴PD⊥面ABE…(5分)
(Ⅱ)解:在底面ABCD中过点C作CM∥AB交AD与点M,在△PAD中过点M作MF∥PA交PD于点F,
连接CF,∴面CMF∥面PAB,∴CF∥面PAB…(7分)
在底面ABCD中,∠CAD=30°,∠ACD=90°,CM⊥AD,故DM=
CD=
DA,∴DF=
DP…(8分)
∴在线段PD上存在点F满足DF=
DP,使CF∥面PAB…(9分)
因此,点F是线段DP靠近点D的一个四等分点,则VD-ACF=VF-ACD=
S△ACD•hF=
S△ACD•PA…(10分)
∵△ABC中,AB=BC=3
且∠ABC=60°,∴AC=3
又在Rt△ACD中,∠CAD=30°,∠ACD=90°,AC=3
,则DC=3,…(11分)
∴S△ACD=
AC•CD=
,则VD-ACF=VF-ACD=
S△ACD•PA=
×
×3
=
…(12分)
 (Ⅰ)证明:∵PA⊥底面ABCD,
(Ⅰ)证明:∵PA⊥底面ABCD,∴PA⊥AB,PA⊥CD
又AB⊥AD,∴AB⊥面PAD,∴AB⊥PD …(2分)
又AC⊥CD,∴CD⊥面PAC,∴CD⊥AE …(3分)
∵PA=AB=BC=AC,E是PC的中点,
∴AE⊥PC,
∵CD∩PC=C,
∴AE⊥面PCD,
∴AE⊥PD …(4分)
∵AB∩AE=A,
∴PD⊥面ABE…(5分)
(Ⅱ)解:在底面ABCD中过点C作CM∥AB交AD与点M,在△PAD中过点M作MF∥PA交PD于点F,
连接CF,∴面CMF∥面PAB,∴CF∥面PAB…(7分)
在底面ABCD中,∠CAD=30°,∠ACD=90°,CM⊥AD,故DM=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∴在线段PD上存在点F满足DF=
| 1 |
| 4 |
因此,点F是线段DP靠近点D的一个四等分点,则VD-ACF=VF-ACD=
| 1 |
| 3 |
| 1 |
| 12 |
∵△ABC中,AB=BC=3
| 3 |
| 3 |
又在Rt△ACD中,∠CAD=30°,∠ACD=90°,AC=3
| 3 |
∴S△ACD=
| 1 |
| 2 |
9
| ||
| 2 |
| 1 |
| 12 |
| 1 |
| 12 |
9
| ||
| 2 |
| 3 |
| 27 |
| 8 |
点评:本题主要考查了线面垂直的判定、以及线面平行的判定,同时考查了空间想象能力,推理论证能力,属于中档题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
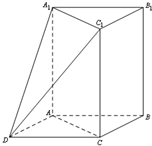 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AC=BC=1,AA1=2.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AC=BC=1,AA1=2.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1.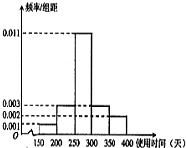 从某节能灯生产线上随机抽取100件产品进行寿命试验,按连续使用时间(单位:天)共分5组,得到频率分布直方图如图.
从某节能灯生产线上随机抽取100件产品进行寿命试验,按连续使用时间(单位:天)共分5组,得到频率分布直方图如图.