题目内容
已知直线y=k(x+4)与圆C:x2+y2+2x-3=0相交于两个不同点A、B,则k的取值范围是 .
考点:直线与圆相交的性质
专题:计算题,直线与圆
分析:利用圆心到直线的距离小于半径,即可求出k的取.值范围
解答:
解:∵圆x2+y2+2x-3=0化成标准方程,得(x+1)2+y2=4
∴圆心坐标为C(-1,0),半径r=2,
∵直线y=k(x+4)与圆C:x2+y2+2x-3=0相交于两个不同点A、B,
∴
<2,
∴-
<k<
,
∴k的取值范围是(-
,
).
故答案为:(-
,
).
∴圆心坐标为C(-1,0),半径r=2,
∵直线y=k(x+4)与圆C:x2+y2+2x-3=0相交于两个不同点A、B,
∴
| |3k| | ||
|
∴-
2
| ||
| 5 |
2
| ||
| 5 |
∴k的取值范围是(-
2
| ||
| 5 |
2
| ||
| 5 |
故答案为:(-
2
| ||
| 5 |
2
| ||
| 5 |
点评:本题给出含有参数的直线与定圆相交,要求参数k的取值范围,着重考查了直线的基本形式、圆的方程和直线与圆的位置关系等知识点,属于基础题.

练习册系列答案
相关题目
在等差数列{an}中,若a2=2,a12=12,那么a4+a19=( )
| A、10 | B、23 | C、28 | D、60 |
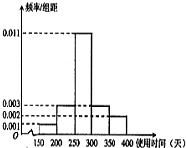 从某节能灯生产线上随机抽取100件产品进行寿命试验,按连续使用时间(单位:天)共分5组,得到频率分布直方图如图.
从某节能灯生产线上随机抽取100件产品进行寿命试验,按连续使用时间(单位:天)共分5组,得到频率分布直方图如图.