题目内容
设函数f(x)=-
a2•x2+lnx.
(1)求函数f(x)的单调递增区间;
(2)若函数f(x)在区间(1,+∞)上是减函数,求a的取值范围.
| 1 |
| 2 |
(1)求函数f(x)的单调递增区间;
(2)若函数f(x)在区间(1,+∞)上是减函数,求a的取值范围.
考点:利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(1)求出函数定义域、函数的导数,分a=0,a>0,a<0三种情况讨论,在定义域内解不等式f′(x)>0即可;
(2)由题意知(1,+∞)为函数f(x)减区间的子集,由(1)问题可得函数的单调减区间,然后由包含关系可得不等式;
(2)由题意知(1,+∞)为函数f(x)减区间的子集,由(1)问题可得函数的单调减区间,然后由包含关系可得不等式;
解答:
解:(1)∵f(x)=-
a2•x2+lnx,其定义域为(0,+∞).
∴f′(x)=-a2•x+
,
①当a=0时,f′(x)=
>0,f(x)的单调递增区间为(0,+∞);
②当a>0时,f′(x)=-a2•x+
=
=
,
则当x∈(0,
)时,f′(x)>0,此时f(x)的单调递增区间为(0,
);
③当a<0时,f′(x)=-a2•x+
=
=
,
则当x∈(0,-
)时,f′(x)>0,此时f(x)的单调递增区间为(0,-
).
(2)由(1)知,当a=0时,f(x)的单调递增区间为(0,+∞),不合题意.
当a>0时,f(x)在(
,+∞)上单调递减,
∴
≤1,解得a≥1;
当a<0时,f(x)在(-
,+∞)上单调递减,
∴-
≤1,解得a≤-1.
综上:a的取值范围是(-∞,-1]∪[1,+∞).
| 1 |
| 2 |
∴f′(x)=-a2•x+
| 1 |
| x |
①当a=0时,f′(x)=
| 1 |
| x |
②当a>0时,f′(x)=-a2•x+
| 1 |
| x |
| -a2x2+1 |
| x |
-a2(x+
| ||||
| x |
则当x∈(0,
| 1 |
| a |
| 1 |
| a |
③当a<0时,f′(x)=-a2•x+
| 1 |
| x |
| -a2x2+1 |
| x |
-a2(x-
| ||||
| x |
则当x∈(0,-
| 1 |
| a |
| 1 |
| a |
(2)由(1)知,当a=0时,f(x)的单调递增区间为(0,+∞),不合题意.
当a>0时,f(x)在(
| 1 |
| a |
∴
| 1 |
| a |
当a<0时,f(x)在(-
| 1 |
| a |
∴-
| 1 |
| a |
综上:a的取值范围是(-∞,-1]∪[1,+∞).
点评:该题考查利用导数研究函数的单调性,属中档题,函数f(x)在区间(a,b)上单调,则(a,b)为f(x)减区间的子集.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
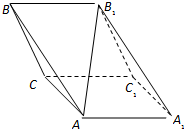 如图,斜三棱柱ABC-A1B1C1,已知侧面BB1C1C与底面ABC垂直且∠BCA=90°,∠B1BC=60°,BC=BB1=2,若二面角A-B1B-C为30°,
如图,斜三棱柱ABC-A1B1C1,已知侧面BB1C1C与底面ABC垂直且∠BCA=90°,∠B1BC=60°,BC=BB1=2,若二面角A-B1B-C为30°,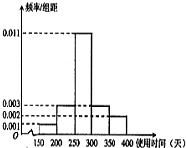 从某节能灯生产线上随机抽取100件产品进行寿命试验,按连续使用时间(单位:天)共分5组,得到频率分布直方图如图.
从某节能灯生产线上随机抽取100件产品进行寿命试验,按连续使用时间(单位:天)共分5组,得到频率分布直方图如图.