题目内容
已知定义域为R的函数f(x)满足:
①f(x+y)=f(x)•f(y)对任何实数x、y都成立;
②存在实数x1、x2使,f(x1)≠f(x2).
求证:
(1)f(0)=1;
(2)f(x)>0.
①f(x+y)=f(x)•f(y)对任何实数x、y都成立;
②存在实数x1、x2使,f(x1)≠f(x2).
求证:
(1)f(0)=1;
(2)f(x)>0.
考点:抽象函数及其应用
专题:证明题,函数的性质及应用
分析:(1)令x=y=0,求出f(0),注意条件②的运用,舍去一个;
(2)将x,y均换成
,得到f(x)=f2(
)即f(x)≥0,注意运用条件②,舍去f(x)=0,即可得证.
(2)将x,y均换成
| x |
| 2 |
| x |
| 2 |
解答:
证明:(1)令x=y=0则f(0)=f2(0),
∴f(0)=0或f(0)=1
若f(0)=0则令y=0,即有f(x)=f(x)•f(0)=0对x∈R均成立,与②矛盾,
故f(0)≠0,
若f(0)=1,则f(x)=f(x)成立,
∴f(0)=1;
(2)将x,y均换成
,则
f(x)=f2(
)即f(x)≥0,
若f(x)=0这与②矛盾,
∴f(x)>0成立.
∴f(0)=0或f(0)=1
若f(0)=0则令y=0,即有f(x)=f(x)•f(0)=0对x∈R均成立,与②矛盾,
故f(0)≠0,
若f(0)=1,则f(x)=f(x)成立,
∴f(0)=1;
(2)将x,y均换成
| x |
| 2 |
f(x)=f2(
| x |
| 2 |
若f(x)=0这与②矛盾,
∴f(x)>0成立.
点评:本题主要考查解决抽象函数的常用方法:赋值法和赋式法,正确赋值和赋式是解题的关键,注意条件的充分运用.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
已知m>0,n>0,
+
=1,则(m+1)(n+4)的最小值为( )
| 1 |
| m |
| 4 |
| n |
| A、49 | B、7 | C、36 | D、6 |
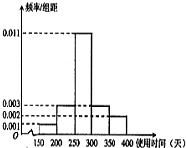 从某节能灯生产线上随机抽取100件产品进行寿命试验,按连续使用时间(单位:天)共分5组,得到频率分布直方图如图.
从某节能灯生产线上随机抽取100件产品进行寿命试验,按连续使用时间(单位:天)共分5组,得到频率分布直方图如图.