题目内容
设函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,-π<φ<π)在x=
处取得最大值3,其图象与x轴的相邻两个交点的距离为
.
(1)求f(x)的解析式;
(2)求f(x)的单调增区间;
(3)当
≤x≤
时,求f(x)的取值范围.
| 5π |
| 12 |
| π |
| 2 |
(1)求f(x)的解析式;
(2)求f(x)的单调增区间;
(3)当
| π |
| 4 |
| π |
| 2 |
考点:函数y=Asin(ωx+φ)的图象变换,由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:(1)依题意,可知A=3,T=
=π,可求得ω=2;再由f(
)=3,-π<φ<π,可求得φ,于是可得f(x)的解析式;
(2)利用正弦函数的单调性可得f(x)的单调增区间;
(3)当
≤x≤
时,
≤2x-
≤
,于是可求
≤3sin(2x-
)≤3,从而可得f(x)的取值范围.
| 2π |
| ω |
| 5π |
| 12 |
(2)利用正弦函数的单调性可得f(x)的单调增区间;
(3)当
| π |
| 4 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
| 3 |
| 2 |
| π |
| 3 |
解答:
解:(1)依题意得A=3,
=
,
∴T=
=π,
解得:ω=2;
又2×
+φ=2kπ+
(k∈Z),
∴φ=2kπ-
(k∈Z),又-π<φ<π,
∴φ=-
,
∴f(x)=3sin(2x-
);
(2)由2kπ-
≤2x-
≤2kπ+
,(k∈Z)
得kπ-
≤x≤kπ+
,(k∈Z)
∴f(x)的单调增区间为[kπ-
,kπ+
](k∈Z);
(3)当
≤x≤
时,
≤2x-
≤
,
∴
≤3sin(2x-
)≤3,即f(x)的取值范围为[
,3].
| T |
| 2 |
| π |
| 2 |
∴T=
| 2π |
| ω |
解得:ω=2;
又2×
| 5π |
| 12 |
| π |
| 2 |
∴φ=2kπ-
| π |
| 3 |
∴φ=-
| π |
| 3 |
∴f(x)=3sin(2x-
| π |
| 3 |
(2)由2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
得kπ-
| π |
| 12 |
| 5π |
| 12 |
∴f(x)的单调增区间为[kπ-
| π |
| 12 |
| 5π |
| 12 |
(3)当
| π |
| 4 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
∴
| 3 |
| 2 |
| π |
| 3 |
| 3 |
| 2 |
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查正弦函数的单调性及最值,属于中档题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
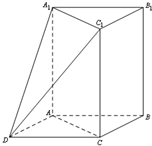 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AC=BC=1,AA1=2.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠ACB=90°,AC=BC=1,AA1=2.以AB,BC为邻边作平行四边形ABCD,连接DA1和DC1.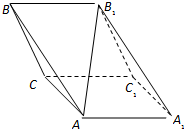 如图,斜三棱柱ABC-A1B1C1,已知侧面BB1C1C与底面ABC垂直且∠BCA=90°,∠B1BC=60°,BC=BB1=2,若二面角A-B1B-C为30°,
如图,斜三棱柱ABC-A1B1C1,已知侧面BB1C1C与底面ABC垂直且∠BCA=90°,∠B1BC=60°,BC=BB1=2,若二面角A-B1B-C为30°,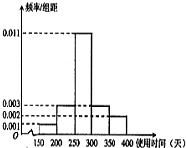 从某节能灯生产线上随机抽取100件产品进行寿命试验,按连续使用时间(单位:天)共分5组,得到频率分布直方图如图.
从某节能灯生产线上随机抽取100件产品进行寿命试验,按连续使用时间(单位:天)共分5组,得到频率分布直方图如图.