��Ŀ����
��֪������C1��y2=8x��˫����C2��
-
=1��a��0��b��0���й�������F2����A������C1��C2�ڵ�һ���Ľ��㣬��|AF2|=5��
��1����˫���߽���F2����һ����F1������͵�A�����ꣻ
��2����˫����C2�ķ��̣�
��3����F1ΪԲ�ĵ�ԲM��ֱ��y=
x���У�ԲN����x-2��2+y2=1������P��1��
�������ഹֱ�ҷֱ���ԲM��ԲN�ཻ��ֱ��l1��l2����l1��ԲM�صõ��ҳ�Ϊs��l2��ԲN�صõ��ҳ�Ϊt���ʣ�
�Ƿ�Ϊ��ֵ������ǣ�����������ֵ��������ǣ���˵�����ɣ�
| x2 |
| a2 |
| y2 |
| b2 |
��1����˫���߽���F2����һ����F1������͵�A�����ꣻ
��2����˫����C2�ķ��̣�
��3����F1ΪԲ�ĵ�ԲM��ֱ��y=
| 3 |
| 3 |
| s |
| t |
���㣺ֱ����Բ���ߵ��ۺ�����
ר�⣺Բ�����е���ֵ�뷶Χ����
��������1����������C1��y2=8x�Ľ��������˫���߽���F2����һ����F1�����꣬�������߶����������A�����꣮
��2������֪�����Ƶ���
���ɴ������˫����C2�ķ��̣�
��3����ԲM�ķ���Ϊ����x+2��2+y2=r2����l1�ķ���Ϊkx-y+
-k=0����l2�ķ���x+ky-
k-1=0���ɴ����õ㵽ֱ�߾��빫ʽ�����֪���������
�Ƕ�ֵ
��
��2������֪�����Ƶ���
|
��3����ԲM�ķ���Ϊ����x+2��2+y2=r2����l1�ķ���Ϊkx-y+
| 3 |
| 3 |
| s |
| t |
| 3 |
���
�⣺��1����������C1��y2=8x�Ľ���ΪF2��2��0����
��˫����C2�Ľ���ΪF1��-2��0����F2��2��0����
��A��x0��y0������A��������C1��y2=8x�ϣ���|AF2|=5��
�������߶����x0+2=5����x0=3��y02=8��3����y0=��2
��
��A��3��2
����A��3��-2
����
��2���ɣ�1��֪˫���ߵİ뽹��c=2����˫���߹����㣬
��
�����a=1��b=
��
��˫����C2�ķ���Ϊx2-
=1��
��3��
Ϊ��ֵ��˵�����£�
��ԲM�ķ���Ϊ����x+2��2+y2=r2��
��ԲM��ֱ��y=
x����
��ԲM�İ뾶Ϊr=
=
��
��ԲM����x+2��2+y2=3��
������֪��ֱ��l1��ֱ�߲�����ʱ���������⣬
��l1��ֱ�ߵ�б�ʴ��ڣ���l1�ķ���Ϊy-
=k(x-1)��
��kx-y+
-k=0��
��l2�ķ���Ϊy-
=-
(x-1)����x+ky-
k-1=0��
���F1��ֱ��l1�ľ���Ϊd1=
��
��F2��ֱ��l2�ľ���Ϊd2=
��
��ֱ��l1��ԲM�صõ��ҳ�S=2
=2
��
ֱ��l2��Բ�صõ��ҳ�t=2
=1
��
��
=
=
=
��
��
�Ƕ�ֵ
��
��˫����C2�Ľ���ΪF1��-2��0����F2��2��0����
��A��x0��y0������A��������C1��y2=8x�ϣ���|AF2|=5��
�������߶����x0+2=5����x0=3��y02=8��3����y0=��2
| 6 |
��A��3��2
| 6 |
| 6 |
��2���ɣ�1��֪˫���ߵİ뽹��c=2����˫���߹����㣬
��
|
| 3 |
��˫����C2�ķ���Ϊx2-
| y2 |
| 3 |
��3��
| s |
| t |
��ԲM�ķ���Ϊ����x+2��2+y2=r2��
��ԲM��ֱ��y=
| 3 |
��ԲM�İ뾶Ϊr=
2
| ||||
|
| 3 |
��ԲM����x+2��2+y2=3��
������֪��ֱ��l1��ֱ�߲�����ʱ���������⣬
��l1��ֱ�ߵ�б�ʴ��ڣ���l1�ķ���Ϊy-
| 3 |
��kx-y+
| 3 |
��l2�ķ���Ϊy-
| 3 |
| 1 |
| k |
| 3 |
���F1��ֱ��l1�ľ���Ϊd1=
|3k-
| ||
|
��F2��ֱ��l2�ľ���Ϊd2=
|
| ||
|
��ֱ��l1��ԲM�صõ��ҳ�S=2
3-(
|
|
ֱ��l2��Բ�صõ��ҳ�t=2
1-(
|
|
��
| S |
| t |
|
|
| 3 |
��
| s |
| t |
| 3 |
���������⿼���������������˫���߷��̵������������ҳ��ı�ֵ�Ƿ�Ϊ��ֵ���ж���������ʱҪ�������⣬ע��㵽ֱ�ߵľ��빫ʽ�ĺ������ã�

��ϰ��ϵ�д�
 �ظ���ʦ�㲦ϵ�д�
�ظ���ʦ�㲦ϵ�д�
�����Ŀ
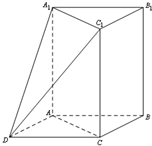 ��ͼ��������ABC-A1B1C1�У�AA1��ƽ��ABC����ACB=90�㣬AC=BC=1��AA1=2����AB��BCΪ�ڱ���ƽ���ı���ABCD������DA1��DC1��
��ͼ��������ABC-A1B1C1�У�AA1��ƽ��ABC����ACB=90�㣬AC=BC=1��AA1=2����AB��BCΪ�ڱ���ƽ���ı���ABCD������DA1��DC1��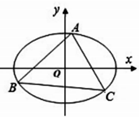 ��֪��ԲC��
��֪��ԲC��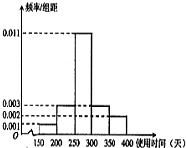 ��ij���ܵ��������������ȡ100����Ʒ�����������飬������ʹ��ʱ�䣨��λ���죩����5�飬�õ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��
��ij���ܵ��������������ȡ100����Ʒ�����������飬������ʹ��ʱ�䣨��λ���죩����5�飬�õ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��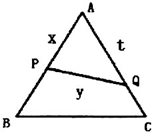 ��֪��ABC�DZ߳�Ϊ2���������Σ�P��Q������AB��AC���ϵĵ㣬���߶�PQ����ABC�ֳ������ȵ������֣���AP=x��AQ=t��PQ=y����
��֪��ABC�DZ߳�Ϊ2���������Σ�P��Q������AB��AC���ϵĵ㣬���߶�PQ����ABC�ֳ������ȵ������֣���AP=x��AQ=t��PQ=y����