题目内容
观察下列等式23=3+5，33=7+9+11，43=13+15+17+19，53=21+23+25+27+29，…，若类似上面各式方法将m3分拆得到的等式右边最后一个数是131，则正整数m等于 ．
考点：归纳推理
专题：推理和证明
分析：可得规律：第n行的左边是m3，右边是m个连续奇数的和，设第m行的第一个数为an，累加可得an，（最后一个数131）
解答：
解：由题意可得第n行的左边是m3，右边是m个连续奇数的和，
设第n行的最后一个数为an，则有a2-a1=11-5=6=1×2+4，
a3-a2=19-11=8=2×2+4，
…
an-an-1=（n-1）×2+4，
∴（a2-a1）+（a3-a2）+…+an-an-1=1×2+4+2×2+4+…+（n-1）×2+4，
∴an-a1=n2+3n-4，
故an=n2+3n+1，
即n2+3n+1=131
解得n=10．
m=n+1=10+1=11
故答案为：11
设第n行的最后一个数为an，则有a2-a1=11-5=6=1×2+4，
a3-a2=19-11=8=2×2+4，
…
an-an-1=（n-1）×2+4，
∴（a2-a1）+（a3-a2）+…+an-an-1=1×2+4+2×2+4+…+（n-1）×2+4，
∴an-a1=n2+3n-4，
故an=n2+3n+1，
即n2+3n+1=131
解得n=10．
m=n+1=10+1=11
故答案为：11
点评：本题考查类比推理，涉及累加法求数列的通项公式，属基础题．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
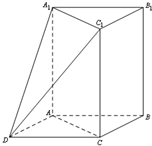如图，三棱柱ABC-A1B1C1中，AA1⊥平面ABC，∠ACB=90°，AC=BC=1，AA1=2．以AB，BC为邻边作平行四边形ABCD，连接DA1和DC1．
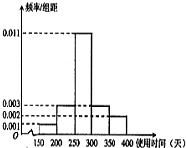从某节能灯生产线上随机抽取100件产品进行寿命试验，按连续使用时间（单位：天）共分5组，得到频率分布直方图如图．
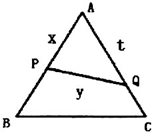已知△ABC是边长为2的正三角形，P、Q依次是AB、AC边上的点，且线段PQ将△ABC分成面积相等的两部分．设AP=x，AQ=t，PQ=y，求：
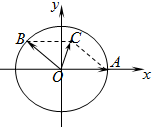如图，在xOy平面上，点A（1，0），点B在单位圆上，∠AOB=θ（0＜θ＜π），若