Question

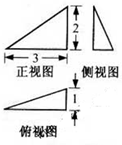已知某三棱锥的三视图（单位：cm）如图所示，则该三棱锥的外接球的表面积等于

 

cm³．

Answer 1

考点：由三视图求面积、体积

专题：计算题,空间位置关系与距离

分析：几何体是三棱锥，根据三视图判断几何体的结构特征，结合直观图判断三视图的数据所对应的几何量，求得外接球的半径，代入球的表面积公式计算．

解答： 解：由三视图知：几何体是三棱锥，如图：

其中SA⊥平面ABC，CB⊥平面SAB，∴外接球的球心为SC的中点，
∴外接球的半径R=

9+4+1

2

=

14

2

，
∴外接球的表面积S=4π×

14

4

=14π．
故答案为：14π．

点评：本题考查了由三视图求几何体的外接球的表面积，根据三视图判断几何体的结构特征是解答本题的关键．