题目内容
已知数列{an}中,a1=1,a2=2,设Sn为数列{an}的前n项和,对于任意的n≥2,n∈N+,Sn+1+Sn-1=2(Sn+1)都成立,则Sn= .
考点:数列递推式
专题:计算题,等差数列与等比数列
分析:由Sn+1+Sn-1=2(Sn+1),得Sn+1-Sn=Sn-Sn-1+2,可判断{Sn+1-Sn}是首项为S2-S1=2,公差为2的等差数列,从而Sn+1-Sn=2+(n-1)×2=2n,然后利用累加法可求答案.
解答:
解:由Sn+1+Sn-1=2(Sn+1),得Sn+1-Sn=Sn-Sn-1+2,
∴{Sn+1-Sn}是首项为S2-S1=2,公差为2的等差数列,
∴Sn+1-Sn=2+(n-1)×2=2n,
则n≥2时,S2-S1=2,S3-S2=4,…,Sn-Sn-1=2(n-1),
累加,得Sn-S1=2+4+…+2(n-1)=
=n2-n,
∴sn=n2-n+1,又s1=1适合上式,
故sn=n2-n+1,
故答案为:n2-n+1.
∴{Sn+1-Sn}是首项为S2-S1=2,公差为2的等差数列,
∴Sn+1-Sn=2+(n-1)×2=2n,
则n≥2时,S2-S1=2,S3-S2=4,…,Sn-Sn-1=2(n-1),
累加,得Sn-S1=2+4+…+2(n-1)=
| (n-1)2n |
| 2 |
∴sn=n2-n+1,又s1=1适合上式,
故sn=n2-n+1,
故答案为:n2-n+1.
点评:本题考查由数列递推式求数列通项,累加法求数列的通项是常用方法,要熟练掌握.

练习册系列答案
相关题目
设i是虚数单位,复数Z=
,则
=( )
| 2 |
| 1+i |
. |
| Z |
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |
设数列{an}满足a1=2,an+1=4an-3n+1,n∈N*,则数列{an}的前n项和可以表示为( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
 如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的平均数为17,乙组数据的中位数为17,则xy=
如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的平均数为17,乙组数据的中位数为17,则xy=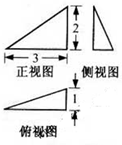 已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的外接球的表面积等于
已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的外接球的表面积等于 如图,已知△ABC(|
如图,已知△ABC(|