题目内容
已知直线x=1与函数f(x)=2x,g(x)=log2(x+2),h(x)=
x+1的图象依次交于M,N,P三点,则关于M,N,P三点的纵坐标yM,yN,yP的说法正确的是( )
| 1 |
| 2 |
| A、yN>yM>yP |
| B、yP>yN>yM |
| C、yM>yN>yP |
| D、yM>yP>yN |
考点:函数的图象
专题:函数的性质及应用
分析:由题设,先计算出三点的纵坐标,再比较它们的大小即可得出正确选项
解答:
解:由题意,当x=1时,yM=2,yN=log23<2,yP=
=log22
<log23,
所以有yM>yN>yP,
故选:C
| 3 |
| 2 |
| 2 |
所以有yM>yN>yP,
故选:C
点评:本题考查函数的图象与直线x=1的交点的纵坐标的求法,掌握对数值大小比较的方法是解答本题的关键.

练习册系列答案
相关题目
设i是虚数单位,复数Z=
,则
=( )
| 2 |
| 1+i |
. |
| Z |
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |
已知一个凸多面体的三视图如图,则它的体积为( )


| A、6 | ||
| B、7 | ||
C、
| ||
D、
|
函数y=2 |log2x|的图象大致是( )
A、 |
B、 |
C、 |
D、 |
若x,y满足约束条件
,且z=kx+y取得最小值是的点有无数个,则k=( )
|
| A、-1 | B、2 |
| C、-1或2 | D、1或-2 |
设数列{an}满足a1=2,an+1=4an-3n+1,n∈N*,则数列{an}的前n项和可以表示为( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
已知
=(3,2),
=(-2,3),则
与
的关系是( )
| a |
| b |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
| D、没有关系 |
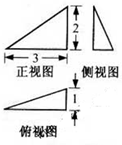 已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的外接球的表面积等于
已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的外接球的表面积等于