题目内容
过点P(2,3)且与直线2x+y-1=0垂直的直线方程是 .
考点:直线的一般式方程与直线的垂直关系
专题:直线与圆
分析:与直线l:2x+y-1=0垂直的直线的斜率k=
,由此能求出过点P(2,3)且与直线l:2x+y-1=0垂直的直线方程.
| 1 |
| 2 |
解答:
解:∵与直线l:2x+y-1=0垂直的直线的斜率k=
,
∴过点P(2,3)与直线l:2x+y-1=0垂直的直线方程为:
y-3=
(x-2),整理,得x-2y+4=0.
故答案为:x-2y+4=0.
| 1 |
| 2 |
∴过点P(2,3)与直线l:2x+y-1=0垂直的直线方程为:
y-3=
| 1 |
| 2 |
故答案为:x-2y+4=0.
点评:本题考查直线方程的求法,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
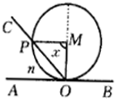 如图所示,半径为2的⊙M切直线AB于O,射线OC从OA出发绕着O点顺时针旋转到OB.旋转过程中,OC交⊙M于P.记∠PMO为x,弓形PnO的面积为S=f(x),那么f(x)的图象是下图中的( )
如图所示,半径为2的⊙M切直线AB于O,射线OC从OA出发绕着O点顺时针旋转到OB.旋转过程中,OC交⊙M于P.记∠PMO为x,弓形PnO的面积为S=f(x),那么f(x)的图象是下图中的( )A、 |
B、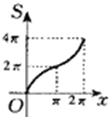 |
C、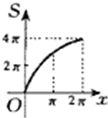 |
D、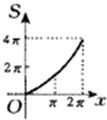 |
设复数z1=1-ai,z2=(2+i)2(i为虚数单位),若复数
在复平面内对应的点在直线5x-5y+3=0上,则a=( )
| z1 |
| z2 |
| A、6 | B、-6 | C、-22 | D、22 |
 如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的平均数为17,乙组数据的中位数为17,则xy=
如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的平均数为17,乙组数据的中位数为17,则xy=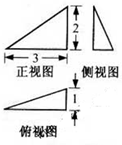 已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的外接球的表面积等于
已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的外接球的表面积等于