题目内容
在△ABC中,已知a,b,c分别是角A,B,C的对边,且2cosBcosC(1-tanBtanC)=1.
(1)求角A的大小;
(2)若a=2
,△ABC的面积为2
,求b+c的值.
(1)求角A的大小;
(2)若a=2
| 7 |
| 3 |
考点:正弦定理,余弦定理
专题:三角函数的求值
分析:(1)已知等式括号中第二项利用同角三角函数间基本关系切化弦后,整理求出cos(B+C)的值,进而求出cosA的值,确定出A的度数;
(2)利用三角形面积公式表示出三角形ABC面积,将已知面积与sinA的值代入求出bc的值,再利用余弦定理列出关系式,利用完全平方公式变形,将a,bc,以及cosA的值代入,开方即可求出b+c的值.
(2)利用三角形面积公式表示出三角形ABC面积,将已知面积与sinA的值代入求出bc的值,再利用余弦定理列出关系式,利用完全平方公式变形,将a,bc,以及cosA的值代入,开方即可求出b+c的值.
解答:
解:(1)∵2cosBcosC(1-tanBtanC)=2cosBcosC(1-
)=1,
∴2(cosBcosC-sinBsinC)=1,即cos(B+C)=
,
∵B+C=π-A,
∴cosA=-
,
∵A为三角形内角,
∴A=
;
(2)∵sinA=
,S=2
,
∴
bcsinA=2
,即
bc=2
,
∴bc=8,
由余弦定理得:a2=b2+c2-2bccosA=b2+c2+bc=(b+c)2-bc,
将a=2
,bc=8代入得:(b+c)2=36,
解得:b+c=6.
| sinBsinC |
| cosBcosC |
∴2(cosBcosC-sinBsinC)=1,即cos(B+C)=
| 1 |
| 2 |
∵B+C=π-A,
∴cosA=-
| 1 |
| 2 |
∵A为三角形内角,
∴A=
| 2π |
| 3 |
(2)∵sinA=
| ||
| 2 |
| 3 |
∴
| 1 |
| 2 |
| 3 |
| ||
| 4 |
| 3 |
∴bc=8,
由余弦定理得:a2=b2+c2-2bccosA=b2+c2+bc=(b+c)2-bc,
将a=2
| 7 |
解得:b+c=6.
点评:此题考查了正弦、余弦定理,以及三角形的面积公式,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目
给出下列四个结论,其中正确的是( )
| A、“a=3”是“直线l1:a2x+3y-1=0与直线l2:x-3y+2=0垂直”的充要条件 | ||||||
| B、随机变量ξ~N(0,1),若P(|ξ|≤1.96)=0.950,则P(ξ<-1.96)=0.05 | ||||||
| C、对于命题P:?x∈R使得x2+x+1<0,则¬P:?x∈R均有x2+x+1>0 | ||||||
D、在区间[0,1]上随机取一个数x,则sin
|
设i是虚数单位,复数Z=
,则
=( )
| 2 |
| 1+i |
. |
| Z |
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |
 如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的平均数为17,乙组数据的中位数为17,则xy=
如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的平均数为17,乙组数据的中位数为17,则xy=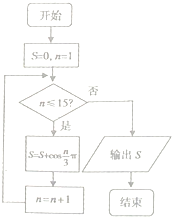
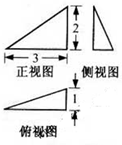 已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的外接球的表面积等于
已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的外接球的表面积等于