题目内容
给出下列四个结论:
①由曲线y=x2、y=1围成的区域的面积为
;
②“x=2”是“向量
=(x-1,1)与向量
=(3,x+1)平行”的充分非必要条件;
③命题“a、b都是有理数”的否定是“a、b都不是有理数”;
④函数f(θ)=sin2θ+
的最小值等于4.
其中正确结论的个数为( )
①由曲线y=x2、y=1围成的区域的面积为
| 1 |
| 3 |
②“x=2”是“向量
| a |
| b |
③命题“a、b都是有理数”的否定是“a、b都不是有理数”;
④函数f(θ)=sin2θ+
| 4 |
| sin2θ |
其中正确结论的个数为( )
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用
专题:阅读型,简易逻辑
分析:①由图可知,可运用定积分先求出曲线与x=-1和y轴围成的区域的面积S,再用矩形的面积减去2S,即得所求的面积;②由向量共线的坐标表示,求出x,再根据充分必要条件的定义即可判断;③由命题的否定判断,注意“都是”的否定是“不都是”;④先应用基本不等式求,注意等号成立的条件,然后运用导数判断单调性,由单调性即可求出最小值.
解答:
解:①由曲线y=x2、y=1围成的区域的面积, 可先求出曲线与x轴以及x=-1、y轴
可先求出曲线与x轴以及x=-1、y轴
围成的区域的面积
x2dx=
x3|
=
,则曲线y=x2、y=1围成的区域的面积为1×2-2×
=
,故①错;
②由向量
=(x-1,1)与向量
=(3,x+1)平行得,(x-1)(x+1)=3,即x=±2,所以“x=2”是“向量
=(x-1,1)与向量
=(3,x+1)平行”的充分非必要条件,故②正确;
③命题“a、b都是有理数”的否定是“a、b不都是有理数”,故③错;
④函数f(θ)=sin2θ+
,0<sin2θ≤1,如果运用基本不等式则sin2θ=2不成立,故最小值不等于4,
令t=sin2θ,则f(t)=t+
(0<t≤1),由于f′(t)=1-
<0,即(0,1]为减区间,故最小值为1+4=5,故④错.
故正确个数为1.
故选A.
 可先求出曲线与x轴以及x=-1、y轴
可先求出曲线与x轴以及x=-1、y轴围成的区域的面积
| ∫ | 0 -1 |
| 1 |
| 3 |
0 -1 |
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
②由向量
| a |
| b |
| a |
| b |
③命题“a、b都是有理数”的否定是“a、b不都是有理数”,故③错;
④函数f(θ)=sin2θ+
| 4 |
| sin2θ |
令t=sin2θ,则f(t)=t+
| 4 |
| t |
| 4 |
| t2 |
故正确个数为1.
故选A.
点评:本题主要考查充分必要条件的判断和命题的否定,注意与否命题的区别,同时考查定积分运用求不规则图象的面积,以及应用基本不等式求最值的注意点,是一道易错题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
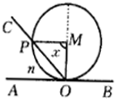 如图所示,半径为2的⊙M切直线AB于O,射线OC从OA出发绕着O点顺时针旋转到OB.旋转过程中,OC交⊙M于P.记∠PMO为x,弓形PnO的面积为S=f(x),那么f(x)的图象是下图中的( )
如图所示,半径为2的⊙M切直线AB于O,射线OC从OA出发绕着O点顺时针旋转到OB.旋转过程中,OC交⊙M于P.记∠PMO为x,弓形PnO的面积为S=f(x),那么f(x)的图象是下图中的( )A、 |
B、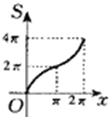 |
C、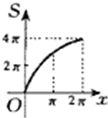 |
D、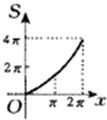 |
给出下列四个结论,其中正确的是( )
| A、“a=3”是“直线l1:a2x+3y-1=0与直线l2:x-3y+2=0垂直”的充要条件 | ||||||
| B、随机变量ξ~N(0,1),若P(|ξ|≤1.96)=0.950,则P(ξ<-1.96)=0.05 | ||||||
| C、对于命题P:?x∈R使得x2+x+1<0,则¬P:?x∈R均有x2+x+1>0 | ||||||
D、在区间[0,1]上随机取一个数x,则sin
|
设i是虚数单位,
表示复数z的共轭复数.若z=1+i,则
+i•
=( )
. |
| z |
| z |
| i |
. |
| z |
| A、-2 | B、-2i | C、2 | D、2i |
已知集合A={x|x>1},B={x||x|<2 },则A∩B等于( )
| A、{x|-1<x<2} |
| B、{x|x>-1} |
| C、{x|-1<x<1} |
| D、{x|1<x<2} |
设复数z1=1-ai,z2=(2+i)2(i为虚数单位),若复数
在复平面内对应的点在直线5x-5y+3=0上,则a=( )
| z1 |
| z2 |
| A、6 | B、-6 | C、-22 | D、22 |
 如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的平均数为17,乙组数据的中位数为17,则xy=
如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的平均数为17,乙组数据的中位数为17,则xy=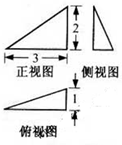 已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的外接球的表面积等于
已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的外接球的表面积等于