题目内容
若函数y=e-x在点(0,1)处的切线为l,则由曲线y=e-x,直线x=1,切线l所围成封闭图形的面积为 .
考点:定积分在求面积中的应用
专题:导数的综合应用
分析:利用导数的几何意义,求出切线方程,利用积分的几何意义,即可求出封闭区域的面积.
解答:
解:∵y=e-x,
∴y′y=-e-x,
则在(0,1)处的切线斜率k=-1,
则切线方程为y-1=-(x-0)=-x,
即y=-x+1,
则阴影部分的面积S=
(e-x)dx-
×1×1=-
e-xd(-x)-
=-e-x|
-
=1-
-
=
-
,
故答案为:
-
∴y′y=-e-x,

则在(0,1)处的切线斜率k=-1,
则切线方程为y-1=-(x-0)=-x,
即y=-x+1,
则阴影部分的面积S=
| ∫ | 1 0 |
| 1 |
| 2 |
| ∫ | 1 0 |
| 1 |
| 2 |
1 0 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| e |
| 1 |
| 2 |
| 1 |
| e |
故答案为:
| 1 |
| 2 |
| 1 |
| e |
点评:本题主要考查导数的几何意义以及积分的几何意义,要求熟练掌握函数的导数公式和积分公式.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
设复数z1=1-ai,z2=(2+i)2(i为虚数单位),若复数
在复平面内对应的点在直线5x-5y+3=0上,则a=( )
| z1 |
| z2 |
| A、6 | B、-6 | C、-22 | D、22 |
若x,y满足约束条件
,且z=kx+y取得最小值是的点有无数个,则k=( )
|
| A、-1 | B、2 |
| C、-1或2 | D、1或-2 |
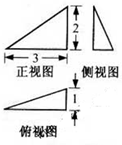 已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的外接球的表面积等于
已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的外接球的表面积等于 如图,已知△ABC(|
如图,已知△ABC(|