题目内容
设函数f(x)=|x-1|+|x-a|,若对x≥1均有f(x)≥4成立,则实数a(a>0)的取值范围为 .
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:由题意可得,当x≥1时,f(x)=|x-1|+|x-a|的最小值大于或等于4.利用绝对值三角不等式求得f(x)的最小值为|a-1|,可得|a-1|≥4,由此求得a的范围.
解答:
解:由题意可得,当x≥1时,f(x)=|x-1|+|x-a|的最小值大于或等于4,
而f(x)=|x-1|+|x-a|≥|(x-1)-(x-a)|=|a-1|,故f(x)=|x-1|+|x-a|的最小值为|a-1|,
∴|a-1|≥4,即a-1≥4,或a-1≤-4.解得 a≥5,或 a≤-3 (舍去).
故实数a(a>0)的取值范围为[5,+∞),
故答案为:[5,+∞).
而f(x)=|x-1|+|x-a|≥|(x-1)-(x-a)|=|a-1|,故f(x)=|x-1|+|x-a|的最小值为|a-1|,
∴|a-1|≥4,即a-1≥4,或a-1≤-4.解得 a≥5,或 a≤-3 (舍去).
故实数a(a>0)的取值范围为[5,+∞),
故答案为:[5,+∞).
点评:本题主要考查绝对值三角不等式,绝对值不等式的解法,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
设i是虚数单位,
表示复数z的共轭复数.若z=1+i,则
+i•
=( )
. |
| z |
| z |
| i |
. |
| z |
| A、-2 | B、-2i | C、2 | D、2i |
已知一个凸多面体的三视图如图,则它的体积为( )


| A、6 | ||
| B、7 | ||
C、
| ||
D、
|
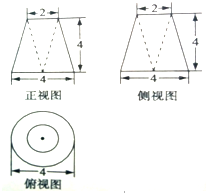
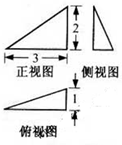 已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的外接球的表面积等于
已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的外接球的表面积等于 如图,已知△ABC(|
如图,已知△ABC(|