题目内容
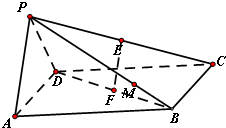 如图,在四棱锥P-ABCD中,底面ABCD是正方形,E,F分别在PC,BD上,
如图,在四棱锥P-ABCD中,底面ABCD是正方形,E,F分别在PC,BD上,| CE |
| CP |
| BF |
| BD |
| 1 |
| 3 |
| 2 |
(1)求证:EF∥平面PAD;
(2)求证:平面PAB⊥平面PCD.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)连结CF,并延长,使其与DA的延长线交于点Q,连结PQ,由已知得EF∥PQ,由此能证明EF∥平面PAD.
(2)由已知得CD⊥平面PAD,从而CD⊥PA,进而△PAD是等腰直角三角形,且∠APD=
,即PA⊥PD,由此能证明平面PAB⊥平面PCD.
(2)由已知得CD⊥平面PAD,从而CD⊥PA,进而△PAD是等腰直角三角形,且∠APD=
| π |
| 2 |
解答:
证明:(1)如图,连结CF,并延长,使其与DA的延长线交于点Q,连结PQ,
∵在正方形ABCD中,BC∥DA,∴BC∥DQ,
∴
=
=
,又
=
,∴
=
,
在△CPQ中,EF∥PQ,
又∵PQ?平面PAD,EF?平面PAD,
∴EF∥平面PAD.
(2)∵平面PAD⊥平面ABCD,
又∵在正方形ABCD中有CD⊥AD,∴CD⊥平面PAD,
∴CD⊥PA,∵PA=PD=
,AD=2,
∴△PAD是等腰直角三角形,且∠APD=
,即PA⊥PD,
又∵CD∩PD=D,∴PA⊥平面PCD,
又∵PA?平面PAB,∴平面PAB⊥平面PCD.
∵在正方形ABCD中,BC∥DA,∴BC∥DQ,

∴
| BE |
| BD |
| CF |
| CQ |
| 1 |
| 3 |
| CE |
| CP |
| 1 |
| 3 |
| CE |
| CP |
| CF |
| CQ |
在△CPQ中,EF∥PQ,
又∵PQ?平面PAD,EF?平面PAD,
∴EF∥平面PAD.
(2)∵平面PAD⊥平面ABCD,
又∵在正方形ABCD中有CD⊥AD,∴CD⊥平面PAD,
∴CD⊥PA,∵PA=PD=
| 2 |
∴△PAD是等腰直角三角形,且∠APD=
| π |
| 2 |
又∵CD∩PD=D,∴PA⊥平面PCD,
又∵PA?平面PAB,∴平面PAB⊥平面PCD.
点评:本题考查线面垂直的证明,考查面面垂直的证明,是中档题,解题时要注意空间中线线、线面、面面间位置关系的合理运用.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
把函数y=sin(2x-
)的图象向左平移
个单位后,所得函数图象的一条对称轴为( )
| π |
| 6 |
| π |
| 6 |
| A、x=0 | ||
B、x=
| ||
C、x=-
| ||
D、x=
|
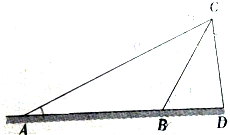 为了测量一个塔的高度,某人站在A处测得塔尖C的仰角为30°,前进100m后达到B处,测得塔尖的仰角为75°,则该塔的高度为
为了测量一个塔的高度,某人站在A处测得塔尖C的仰角为30°,前进100m后达到B处,测得塔尖的仰角为75°,则该塔的高度为