题目内容
已知函数f(x)=2sinωx,其中ω>0,若x1∈[-
π,0),x2∈(0,
],f(x1)=f(x2),则ω的最小值为 .
| 2 |
| 3 |
| π |
| 4 |
考点:正弦函数的图象
专题:函数的性质及应用,三角函数的图像与性质
分析:由函数的奇偶性的定义判断出函数f(x)是奇函数,再由题意和函数的周期公式列出不等式,求出ω的取值范围.
解答:
解:由题意知,函数f(x)=2sinωx是奇函数,
因为存在x1∈[-
π,0),x2∈(0,
],使得f(x1)=f(x2),
所以根据周期函数图象得出:函数f(x)的周期T=
≤
,解得?≥
,
则ω的取值范围为[
,+∞),
故答案为:
.
因为存在x1∈[-
| 2 |
| 3 |
| π |
| 4 |
所以根据周期函数图象得出:函数f(x)的周期T=
| 2π |
| ω |
| 4π |
| 3 |
| 3 |
| 2 |
则ω的取值范围为[
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:本题考查正弦函数的周期性,以及函数的奇偶性的定义,属于中档题.

练习册系列答案
相关题目
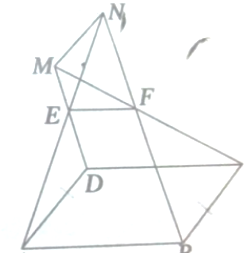 如图所示,若ABCD为平行四边形,EF∥AB,AE与BF相交于点N,DE与CF相交于点M.求证:MN∥AD.
如图所示,若ABCD为平行四边形,EF∥AB,AE与BF相交于点N,DE与CF相交于点M.求证:MN∥AD.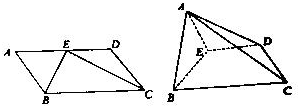 已知:平行四边形ABCD,AB=1,BC=2,∠BAD=60°,E为AD中点.将?ABCD沿BE折成直二面角.
已知:平行四边形ABCD,AB=1,BC=2,∠BAD=60°,E为AD中点.将?ABCD沿BE折成直二面角.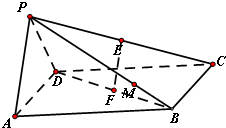 如图,在四棱锥P-ABCD中,底面ABCD是正方形,E,F分别在PC,BD上,
如图,在四棱锥P-ABCD中,底面ABCD是正方形,E,F分别在PC,BD上,