题目内容
已知函数f(x)=
+
-lnx-
,其中a∈R,若曲线y=f(x)在点(1,f(1))处的切线垂直于直线x-2y=0,则切线方程为 .
| x |
| 4 |
| a |
| x |
| 3 |
| 2 |
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:由曲线y=f(x)在点(1,f(1))处的切线垂直于直线x-2y=0可得f′(1)=-2,可求出a的值,可得切点坐标,即可求出切线方程.
解答:
解:(Ⅰ)∵f(x)=
+
-lnx-
,
∴f′(x)=
-
-
,
∵曲线y=f(x)在点(1,f(1))处的切线垂直于直线x-2y=0,
∴f′(1)=
-a-1=-2,
解得:a=
,
∴f(1)=0,
∴切线方程为y=-2(x-1),即2x+y-2=0.
故答案为:2x+y-2=0.
| x |
| 4 |
| a |
| x |
| 3 |
| 2 |
∴f′(x)=
| 1 |
| 4 |
| a |
| x2 |
| 1 |
| x |
∵曲线y=f(x)在点(1,f(1))处的切线垂直于直线x-2y=0,
∴f′(1)=
| 1 |
| 4 |
解得:a=
| 5 |
| 4 |
∴f(1)=0,
∴切线方程为y=-2(x-1),即2x+y-2=0.
故答案为:2x+y-2=0.
点评:本题考查的知识点是利用导数研究曲线上某点切线方程,求出a是关键,难度中档.

练习册系列答案
相关题目
从四面体的四个面中任意取出一个面,这个面的形状恰好为直角三角形的概率最大值为( )
| A、1 | ||
B、
| ||
C、
| ||
D、
|
已知椭圆
+
=1(a>b>0)的半焦距为c(c>0),左焦点为F,右顶点为A,抛物线y2=
(a+c)x与椭圆交于B、C两点,若四边形ABFC是菱形,则椭圆的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
| 15 |
| 8 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知命题“若a,b,c成等比数列,则b2=ac”在它的逆命题、否命题,逆否命题中,真命题的个数是( )
| A、0 | B、1 | C、2 | D、3 |
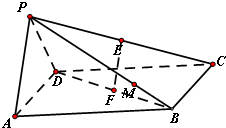 如图,在四棱锥P-ABCD中,底面ABCD是正方形,E,F分别在PC,BD上,
如图,在四棱锥P-ABCD中,底面ABCD是正方形,E,F分别在PC,BD上,