题目内容
把函数y=sin(2x-
)的图象向左平移
个单位后,所得函数图象的一条对称轴为( )
| π |
| 6 |
| π |
| 6 |
| A、x=0 | ||
B、x=
| ||
C、x=-
| ||
D、x=
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:由条件利用函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,可得结论.
解答:
解:把函数y=sin(2x-
)的图象向左平移
个单位后,得到函数y=sin[2(x+
)-
]=sin(2x+
)的图象,
令x=
,求得y=sin(2x+
)=1,是最大值,可得所得函数图象的一条对称轴为x=
,
故选:B.
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
令x=
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
故选:B.
点评:本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于基础题.

练习册系列答案
相关题目
已知命题“若a,b,c成等比数列,则b2=ac”在它的逆命题、否命题,逆否命题中,真命题的个数是( )
| A、0 | B、1 | C、2 | D、3 |
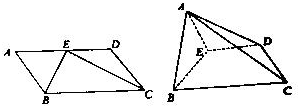 已知:平行四边形ABCD,AB=1,BC=2,∠BAD=60°,E为AD中点.将?ABCD沿BE折成直二面角.
已知:平行四边形ABCD,AB=1,BC=2,∠BAD=60°,E为AD中点.将?ABCD沿BE折成直二面角.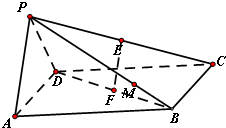 如图,在四棱锥P-ABCD中,底面ABCD是正方形,E,F分别在PC,BD上,
如图,在四棱锥P-ABCD中,底面ABCD是正方形,E,F分别在PC,BD上,