题目内容
?ABCD中，M，N分别为DC，BC的中点，已知
=
，
=
，用
，
表示
= ，
= ．
| AM |
| c |
| AN |
| d |
| c |
| d |
| AB |
| AD |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：如图所示，由
=
，
=
，可得
=
+
=
+
=
，
=
+
=
+
=
，联立解得即可．
| DC |
| AB |
| BC |
| AD |
| AM |
| AD |
| DM |
| AD |
| 1 |
| 2 |
| AB |
| c |
| AN |
| AB |
| BN |
| AB |
| 1 |
| 2 |
| AD |
| d |
解答：
解：如图所示，
∵
=
，
=
，
∴
=
+
=
+
=
，
=
+
=
+
=
，
解得
=
-
，
=
-
，
故答案分别为：
-
；
=
-
．
∵
| DC |
| AB |
| BC |
| AD |
∴
| AM |
| AD |
| DM |
| AD |
| 1 |
| 2 |
| AB |
| c |
| AN |
| AB |
| BN |
| AB |
| 1 |
| 2 |
| AD |
| d |
解得
| AB |
| 4 |
| 3 |
| d |
| 2 |
| 3 |
| c |
| AD |
| 4 |
| 3 |
| c |
| 2 |
| 3 |
| d |
故答案分别为：
| 4 |
| 3 |
| d |
| 2 |
| 3 |
| c |
| AD |
| 4 |
| 3 |
| c |
| 2 |
| 3 |
| d |
点评：本题考查了向量的三角形法则、向量共线定理，属于基础题．
练习册系列答案
相关题目
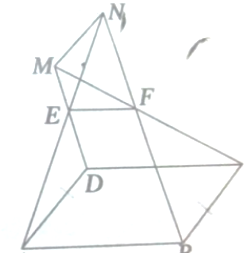如图所示，若ABCD为平行四边形，EF∥AB，AE与BF相交于点N，DE与CF相交于点M．求证：MN∥AD．
如图，圆O是△ABC的外接圆，∠BAC的平分线交BC于点F，D是AF的延长线与⊙O的交点，AC的延线与⊙O的切线DE交于点E．从四面体的四个面中任意取出一个面，这个面的形状恰好为直角三角形的概率最大值为（ ）
| A、1 | ||
B、
| ||
C、
| ||
D、
|
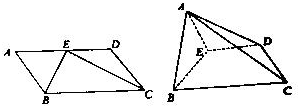已知：平行四边形ABCD，AB=1，BC=2，∠BAD=60°，E为AD中点．将?ABCD沿BE折成直二面角．
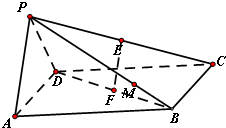如图，在四棱锥P-ABCD中，底面ABCD是正方形，E，F分别在PC，BD上，