题目内容
函数f（x）=
，如果a=f（
），则f（a）= ．
|
| 1 |
| e |
考点：函数的零点,函数的值
专题：函数的性质及应用
分析：先求出a=f（
）的值，再求出f（a）即f（-1）的值即可．
| 1 |
| e |
解答：
解：∵a=f（
）=ln
=-1，
∴f（a）=f（-1）=
，
故答案为：
．
| 1 |
| e |
| 1 |
| e |
∴f（a）=f（-1）=
| 1 |
| e |
故答案为：
| 1 |
| e |
点评：本题考查了求函数值问题，考查了对数，指数的运算，是一道基础题．
练习册系列答案
相关题目
记a=log2
，b=70.3．c=（
）9.1，则a、b、c的大小关系是（ ）
| 5 |
| 6 |
| 1 |
| 7 |
| A、a＜b＜c |
| B、c＜b＜a |
| C、a＜c＜b |
| D、b＜a＜c |
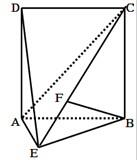如图，直二面角D-AB-E中，四边形ABCD是边长为2的正方形，AE=EB，F为CE上的点，且BF⊥平面ACE，求DE与平面AEC所成夹角的正弦值．
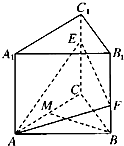如图，直三棱柱ABC-A1B1C1中，CC1=3，底面是边长为2的正三角形，点E，F分别是棱CC1，BB1上的点，点M是线段AC上的动点，EC=2FB．