题目内容
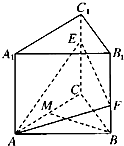如图，直三棱柱ABC-A1B1C1中，CC1=3，底面是边长为2的正三角形，点E，F分别是棱CC1，BB1上的点，点M是线段AC上的动点，EC=2FB．（1）求三棱柱ABC-A1B1C1的表面积；
（2）点M在何位置时，BM∥平面AEF，并证明你的结论．
考点：直线与平面平行的判定,棱柱、棱锥、棱台的体积
专题：空间位置关系与距离
分析：（1）三棱柱ABC-A1B1C1的表面积就是三个侧面面积：3×2×3，+两个底面面积：2×
×2×2×sin
；
（2）因为EC=2FB，所以容易想到取EC中点N，并且使M是AC中点，连接MN，BN，便可得到MN∥AE，BN∥EF，所以根据线面平行和面面平行的判定定理即可得出平面BMN∥平面AEF，所以得到BM∥平面AEF．所以便得出当M在AC中点时，BM∥平面AEF．
| 1 |
| 2 |
| π |
| 3 |
（2）因为EC=2FB，所以容易想到取EC中点N，并且使M是AC中点，连接MN，BN，便可得到MN∥AE，BN∥EF，所以根据线面平行和面面平行的判定定理即可得出平面BMN∥平面AEF，所以得到BM∥平面AEF．所以便得出当M在AC中点时，BM∥平面AEF．
解答：
解：（1）S表=2×
×2×2×sin
+3×2×3=18+2
；
（2）M为AC中点时BM∥平面AEF，证明如下：
如图，取EC的中点N，连接MN，BN；
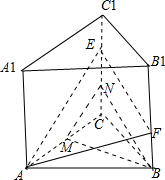
∵M、N分别为AC、EC中点，∴MN∥AE，AE?平面AEF，MN?平面AEF；
∴MN∥平面AEF；
∵EC=2FB，∴EN=FB，且EN∥FB；
∴四边形BFEN为平行四边形，∴BN∥EF，EF?平面AEF，BN?平面AEF；
∴BN∥平面AEF，MN∩BN=N；
∴平面BMN∥平面AEF，BM?平面BMN；
∴BM∥平面AEF．
| 1 |
| 2 |
| π |
| 3 |
| 3 |
（2）M为AC中点时BM∥平面AEF，证明如下：
如图，取EC的中点N，连接MN，BN；
∵M、N分别为AC、EC中点，∴MN∥AE，AE?平面AEF，MN?平面AEF；
∴MN∥平面AEF；
∵EC=2FB，∴EN=FB，且EN∥FB；
∴四边形BFEN为平行四边形，∴BN∥EF，EF?平面AEF，BN?平面AEF；
∴BN∥平面AEF，MN∩BN=N；
∴平面BMN∥平面AEF，BM?平面BMN；
∴BM∥平面AEF．
点评：考查三棱柱的表面积的概念及求法，中位线的性质，线面平行的判定定理，面面平行的判定定理，以及面面平行时其中一平面上的直线和另一平面的关系．
练习册系列答案
相关题目
已知函数f（x）=
，则f[f（-
）]=（ ）
|
| 3 |
| 2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|