题目内容
记a=log2
,b=70.3.c=(
)9.1,则a、b、c的大小关系是( )
| 5 |
| 6 |
| 1 |
| 7 |
| A、a<b<c |
| B、c<b<a |
| C、a<c<b |
| D、b<a<c |
考点:对数值大小的比较
专题:函数的性质及应用
分析:利用对数函数与指数函数的单调性即可得出.
解答:
解:∵a=log2
<0,b=70.3>1,0<c=(
)9.1<1,
∴a<c<b.
故选:C.
| 5 |
| 6 |
| 1 |
| 7 |
∴a<c<b.
故选:C.
点评:本题考查了对数函数与指数函数的单调性,属于基础题.

练习册系列答案
相关题目
若目标函数z=ax+by(a>0,b>0)满足约束条件
且最大值为40,则
+
的最小值为( )
|
| 5 |
| a |
| 1 |
| b |
A、
| ||
B、
| ||
| C、1 | ||
| D、4 |
已知函数f(x)的导函数图象如图所示,若△ABC是以角C为钝角的钝角三角形,则一定成立的是( )
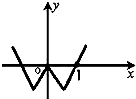

| A、f(sinA)>f(cosB) |
| B、f(sinA)<f(cosB) |
| C、f(sinA)>f(sinB) |
| D、f(cosA)<f(cosB) |
已知互相垂直的两条直线y=kx和y=-
分别与双曲线2x2-y2=1交于点A、B,点P在线段AB上,且满足
•
=
•
,则所有的点P在( )
| x |
| k |
| OA |
| OP |
| OB |
| OP |
| A、双曲线2x2-y2=1上 |
| B、圆x2+y2=1上 |
| C、椭圆上 |
| D、|x|+|y|=1上 |