题目内容
已知四面体ABCD的外接球O,若AB=BC=CA=3,且四面体ABCD的体积的最大值为3
,则球O的表面积为多少?
| 3 |
考点:球的体积和表面积
专题:球
分析:由题意求出球的半径,从而求出球的表面积.
解答:
解:如图示:
 ,
,
∵S△ABC=
×3×
=
,
∴VD-ABC=
×
•DO=3
,
∴设球的半径R,而OA=
,则R2=OA2+(4-R)2,解得R=
,
∴球的表面积S=4πR2=
π.
 ,
,∵S△ABC=
| 1 |
| 2 |
3
| ||
| 2 |
9
| ||
| 4 |
∴VD-ABC=
| 1 |
| 3 |
9
| ||
| 4 |
| 3 |
∴设球的半径R,而OA=
| 3 |
| 19 |
| 8 |
∴球的表面积S=4πR2=
| 361 |
| 16 |
点评:本题考查了球的表面积,考查了四面体的体积,是一道基础题.

练习册系列答案
相关题目
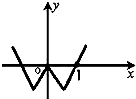
已知函数f(x)的导函数图象如图所示,若△ABC是以角C为钝角的钝角三角形,则一定成立的是( )

| A、f(sinA)>f(cosB) |
| B、f(sinA)<f(cosB) |
| C、f(sinA)>f(sinB) |
| D、f(cosA)<f(cosB) |
化简(
+tanα)cosα等于( )
| 1 |
| tanα |
| A、tanα | ||
B、
| ||
| C、cosα | ||
D、
|