题目内容
求y=x（a-2x）（0＜x＜
，且a为常数）的最大值．
| a |
| 2 |
考点：二次函数在闭区间上的最值,二次函数的性质
专题：计算题,函数的性质及应用
分析：由配方法求函数的最大值，y=x（a-2x）=-2x2+ax=-2（x-
）2+
．
| a |
| 4 |
| a2 |
| 8 |
解答：
解：∵y=x（a-2x）=-2x2+ax
=-2（x-
）2+
，
∵0＜x＜
，
∴当x=
时，函数取得最大值
．
=-2（x-
| a |
| 4 |
| a2 |
| 8 |
∵0＜x＜
| a |
| 2 |
∴当x=
| a |
| 4 |
| a2 |
| 8 |
点评：本题考查了函数的最值的求法，本题应用了配方法，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
已知互相垂直的两条直线y=kx和y=-
分别与双曲线2x2-y2=1交于点A、B，点P在线段AB上，且满足
•
=
•
，则所有的点P在（ ）
| x |
| k |
| OA |
| OP |
| OB |
| OP |
| A、双曲线2x2-y2=1上 |
| B、圆x2+y2=1上 |
| C、椭圆上 |
| D、|x|+|y|=1上 |
已知函数f（x）=
，则f[f（-
）]=（ ）
|
| 3 |
| 2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
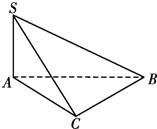已知△ABC中，∠BAC=90°，SA⊥面ABC，且SA=3，AB=AC=4．