题目内容
已知2x+y+a=0与x2+y2-2x+4y=0无公共点,求a的取值范围.
考点:直线与圆的位置关系
专题:直线与圆
分析:由圆的方程,找出圆心和半径,再根据直线与圆相切时,圆心到直线的距离等于圆的半径,列出关于a的方程,求出直线2x+y+a=0与该圆相切时的a值,即可求出直线与圆无公共点时实数a的取值范围.
解答:
解:x2+y2-2x+4y=0的圆心(1,-2)半径为:
.
当直线2x+y+a=0与圆x2+y2-2x+4y=0相切时,
圆心到直线的距离d=r=
,即
=
,
解得:a=±5.
则当直线与圆无公共点时,实数a的范围是a<-5或a>5
a的取值范围:a<-5或a>5.
| 5 |
当直线2x+y+a=0与圆x2+y2-2x+4y=0相切时,
圆心到直线的距离d=r=
| 5 |
| |2-2+a| | ||
|
| 5 |
解得:a=±5.
则当直线与圆无公共点时,实数a的范围是a<-5或a>5
a的取值范围:a<-5或a>5.
点评:此题考查了直线与圆的位置关系,直线与圆相交的性质,点到直线距离公式的应用,其中求出直线与圆相切时a的值是解本题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
若F(
)=x,则下列等式正确的是( )
| 1-x |
| 1+x |
| A、F(2-x)=1-F(x) | ||
B、F(-x)=
| ||
| C、F(x-1)=F(x) | ||
| D、F(F(x))=-x |
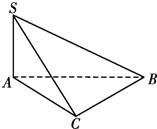 已知△ABC中,∠BAC=90°,SA⊥面ABC,且SA=3,AB=AC=4.
已知△ABC中,∠BAC=90°,SA⊥面ABC,且SA=3,AB=AC=4.