题目内容
10.设l,m,n是三条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )| A. | 若l?β且m∥β,则l∥m | B. | 若l⊥m且l⊥n,则m∥n | ||
| C. | 若m⊥n且m?α,n?β,则l∥α | D. | 若m⊥α且m∥n,n∥β,则α⊥β |
分析 在A中,l与m平行或异面;在B中,m与n相交、平行或异面;在C中,l与α相交、平行或l?α;在D中,由面面垂直的判定定理得α⊥β.
解答 解:由l,m,n是三条不同的直线,α,β是两个不同的平面,知:
在A中,若l?β且m∥β,则l与m平行或异面,故A错误;
在B中,若l⊥m且l⊥n,则m与n相交、平行或异面,故B错误;
在C中,若m⊥n且m?α,n?β,则l与α相交、平行或l?α,故C错误;
在D中,若m⊥α且m∥n,n∥β,则由面面垂直的判定定理得α⊥β,故D正确.
故选:D.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知函数f(x)=log2(x+3)-2x3+4x的图象在[-2,5]内是连续不断的,对应值表如下:
(1)计算上述表格中的对应值a和b.
(2)从上述对应值表中,可以发现函数f(x)在哪几个区间内有零点?说明理由.
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| f(x) | a | -1 | 1.58 | b | -5.68 | -39.42 | -109.19 | -227 |
(2)从上述对应值表中,可以发现函数f(x)在哪几个区间内有零点?说明理由.
5.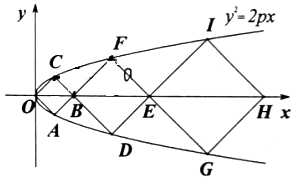 如图所示,O是坐标原点,三个正方形OABC、BDEF、EGHI的顶点中,O、A、C、D、F、G、I七个点都在抛物线y2=2px(p>0)上,另外,B、E、H三个点都在x轴上,则这三个正方形的面积之比( )
如图所示,O是坐标原点,三个正方形OABC、BDEF、EGHI的顶点中,O、A、C、D、F、G、I七个点都在抛物线y2=2px(p>0)上,另外,B、E、H三个点都在x轴上,则这三个正方形的面积之比( )
 如图所示,O是坐标原点,三个正方形OABC、BDEF、EGHI的顶点中,O、A、C、D、F、G、I七个点都在抛物线y2=2px(p>0)上,另外,B、E、H三个点都在x轴上,则这三个正方形的面积之比( )
如图所示,O是坐标原点,三个正方形OABC、BDEF、EGHI的顶点中,O、A、C、D、F、G、I七个点都在抛物线y2=2px(p>0)上,另外,B、E、H三个点都在x轴上,则这三个正方形的面积之比( )| A. | 1:2:3 | B. | 1:4:9 | C. | 2:3:4 | D. | 4:9:16 |
15.函数y=(x2-1)2+2的极值点是( )
| A. | x=1 | B. | x=-1或0 | C. | x=-1或1或0 | D. | x=0或1 |
2.定义在R上的偶函数f(x)满足f(2-x)=f(x),且在[-3,-2]上是减函数,α,β是锐角三角形的两个内角,下列不等式正确的是( )
| A. | f(sinα)>f(cosβ) | B. | f(sinα)<f(cosβ) | C. | f(cosα)<f(cosβ) | D. | f(sinα)>f(sinβ) |
19.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的体积为( )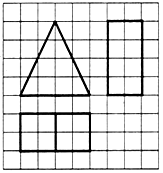

| A. | 16 | B. | $\frac{16}{3}$ | C. | 32 | D. | 48 |