题目内容
1.已知函数f(x)=log2(x+3)-2x3+4x的图象在[-2,5]内是连续不断的,对应值表如下:| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| f(x) | a | -1 | 1.58 | b | -5.68 | -39.42 | -109.19 | -227 |
(2)从上述对应值表中,可以发现函数f(x)在哪几个区间内有零点?说明理由.
分析 (1)利用函数的解析式,直接求解a,b的值即可.
(2)利用零点判定定理判断零点所在区间即可.
解答 解:(1)函数f(x)=log2(x+3)-2x3+4x,
可得:a=f(-2)=log2(-2+3)-2×(-2)3+4×(-2)=8.
b=f(1)=log2(1+3)-2×13+4×1=4.
(2)从上述对应值表中,可以发现函数f(x),
满足f(-2)f(-1)<0;f(-1)f(0)<0;f(1)f(2)<0;
函数的零点存在的区间:(-2,-1);(-1,0);(1,2).
点评 本题考查零点判定定理的应用,函数值的求法,考查计算能力.

练习册系列答案
相关题目
5.在△ABC中,a,b,c分别是内角A,B,C所对的边,已知a=4,B=60°,C=75°,则b=( )
| A. | 2$\sqrt{5}$ | B. | 2$\sqrt{6}$ | C. | 2$\sqrt{3}$ | D. | $\frac{11}{3}$ |
2.设U={1,2,3,4,5},A={1,2,5},B={2,3,4},则B∩∁UA=( )
| A. | ∅ | B. | {2} | C. | {3,4} | D. | {1,3,4,5} |
13.已知双曲线M:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1和双曲线N:$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1,其中b>a>0,双曲线M和双曲线N交于A,B,C,D四个点,且四边形ABCD的面积为4c2,则双曲线M的离心率为( )
| A. | $\frac{\sqrt{5}+3}{2}$ | B. | $\sqrt{5}$+3 | C. | $\frac{\sqrt{5}+1}{2}$ | D. | $\sqrt{5}$+1 |
10.设l,m,n是三条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )
| A. | 若l?β且m∥β,则l∥m | B. | 若l⊥m且l⊥n,则m∥n | ||
| C. | 若m⊥n且m?α,n?β,则l∥α | D. | 若m⊥α且m∥n,n∥β,则α⊥β |
11.已知f(x)=ax2+bx+3a+b是偶函数,定义域为[a-1,2a],则a+b=( )
| A. | $-\frac{1}{3}$ | B. | 1 | C. | 0 | D. | $\frac{1}{3}$ |
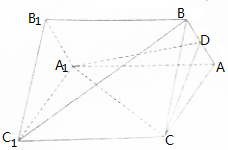 如图,在直三棱柱ABC-A1B1C1中,D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,D是AB的中点.