题目内容
18.已知函数f(x)=-sinx+ax(a为常数).(1)若x∈[0,$\frac{π}{2}$]时函数f(x)单调递增,求实数a的取值范围;
(2)证明:当x∈[0,$\frac{π}{2}$]时,cosx≥-$\frac{1}{2}$x2+1.
分析 (1)求出函数的导数,问题转化为a≥cosx在x∈[0,$\frac{π}{2}$]恒成立,求出a的范围即可;(2)令g(x)=cosx+$\frac{1}{2}$x2-1,根据函数的单调性求出g(x)≥0,从而证出结论即可.
解答 解:(1)函数f(x)=-sinx+ax,f′(x)=-cosx+a,
若x∈[0,$\frac{π}{2}$]时函数f(x)单调递增,
则-cosx+a≥0在x∈[0,$\frac{π}{2}$]恒成立,
则a≥cosx在x∈[0,$\frac{π}{2}$]恒成立,
则a≥1;
(2)证明:令g(x)=cosx+$\frac{1}{2}$x2-1,
则g′(x)=-sinx+x,g″(x)=-cosx+1≥0,
故g′(x)在[0,$\frac{π}{2}$]递增,
故g′(0)≥0,g(x)在[0,$\frac{π}{2}$]递增,
故g(x)≥g(0)0,
故x∈[0,$\frac{π}{2}$]时,cosx≥-$\frac{1}{2}$x2+1.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
1.已知函数f(x)=$\left\{\begin{array}{l}{(2a-1)x+4a,x<1}\\{1+lo{g}_{a}x,x≥1}\end{array}\right.$是R上的减函数,则实数a的取值范围是( )
| A. | [$\frac{1}{6}$,$\frac{1}{3}$) | B. | [$\frac{1}{3}$,$\frac{1}{2}$) | C. | ($\frac{1}{3}$,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,1) |
2.设U={1,2,3,4,5},A={1,2,5},B={2,3,4},则B∩∁UA=( )
| A. | ∅ | B. | {2} | C. | {3,4} | D. | {1,3,4,5} |
13.已知双曲线M:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1和双曲线N:$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1,其中b>a>0,双曲线M和双曲线N交于A,B,C,D四个点,且四边形ABCD的面积为4c2,则双曲线M的离心率为( )
| A. | $\frac{\sqrt{5}+3}{2}$ | B. | $\sqrt{5}$+3 | C. | $\frac{\sqrt{5}+1}{2}$ | D. | $\sqrt{5}$+1 |
3.已知$\overrightarrow{a}$=(cosα,1,sinα),$\overrightarrow{b}$=(sinα,1,cosα),则向量$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-$\overrightarrow{b}$的夹角是( )
| A. | 90° | B. | 60° | C. | 30° | D. | 0° |
10.设l,m,n是三条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )
| A. | 若l?β且m∥β,则l∥m | B. | 若l⊥m且l⊥n,则m∥n | ||
| C. | 若m⊥n且m?α,n?β,则l∥α | D. | 若m⊥α且m∥n,n∥β,则α⊥β |
7.已知f(x)是定义在(0,+∞)上的非负可导函数,且满足xf'(x)+f(x)≤0,对任意的0<a<b,则必有( )
| A. | af(b)≤bf(a) | B. | bf(a)≤af(b) | C. | af(a)≤f(b) | D. | bf(b)≤f(a) |
8.已知圆C1:(x+a)2+(y-2)2=1与圆C2:(x-b)2+(y-2)2=4相外切,a,b为正实数,则ab的最大值为 ( )
| A. | 2$\sqrt{3}$ | B. | $\frac{9}{4}$ | C. | $\frac{3}{2}$ | D. | $\frac{\sqrt{6}}{2}$ |
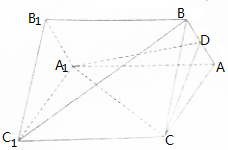 如图,在直三棱柱ABC-A1B1C1中,D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,D是AB的中点.