题目内容

5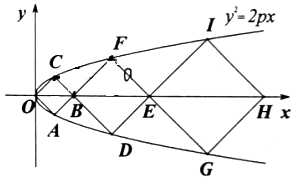．如图所示，O是坐标原点，三个正方形OABC、BDEF、EGHI的顶点中，O、A、C、D、F、G、I七个点都在抛物线y2=2px（p＞0）上，另外，B、E、H三个点都在x轴上，则这三个正方形的面积之比（　　）
A．1：2：3B．1：4：9C．2：3：4D．4：9：16

分析 求出|OB|=4p，|BE|=8p，|EH|=16p，可得这三个正方形的面积之比

解答 解：直线OC的方程为y=x，与抛物线方程联立可得C（2p，2p），
∴B（4p，0）
直线BF的方程为y=x-4p，与抛物线方程联立可得F（8p，4p），
∴E（12p，0），
同理H（28p，0）
∴|OB|=4p，|BE|=8p，|EH|=16p，
∴这三个正方形的面积之比1：4：9，
故选B．

点评 本题考查直线与抛物线的位置关系，考查正方形面积之比，属于中档题．

练习册系列答案
相关题目
8．已知函数f（x）=lg（x2+tx+2）（t为常数，且-2$\sqrt{2}$＜t＜2$\sqrt{2}$）．
（1）当x∈[0，2]时，求函数f（x）的最小值（用t表示）；
（2）是否存在不同的实数a，b，使得f（a）=lga，f（b）=lgb，并且a，b∈（0，2）．若存在，求出实数t的取值范围；若不存在，请说明理由．
9．已知α为△ABC的内角，且tanα=-$\frac{3}{4}$，计算：
（1）$\frac{sinα+cosα}{sinα-cosα}$；
（2）sin（$\frac{π}{2}$+α）-cos（$\frac{π}{2}$-α）．
13．已知双曲线M：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1和双曲线N：$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1，其中b＞a＞0，双曲线M和双曲线N交于A，B，C，D四个点，且四边形ABCD的面积为4c2，则双曲线M的离心率为（　　）
A．$\frac{\sqrt{5}+3}{2}$B．$\sqrt{5}$+3C．$\frac{\sqrt{5}+1}{2}$D．$\sqrt{5}$+1
20．在△ABC中，角A、B、C所对的边分别为a，b，c，且a（sinA-sinB）+bsinB=csinC．
（Ⅰ）求角c的值
（Ⅱ）若2cos2$\frac{A}{2}$-2sin2$\frac{B}{2}$=$\frac{\sqrt{3}}{2}$，且A＜B，求$\frac{c}{a}$的值．
10．设l，m，n是三条不同的直线，α，β是两个不同的平面，下列命题中正确的是（　　）
A．若l?β且m∥β，则l∥mB．若l⊥m且l⊥n，则m∥n
C．若m⊥n且m?α，n?β，则l∥αD．若m⊥α且m∥n，n∥β，则α⊥β
17．抛物线$\frac{1}{4}$y=x2的焦点坐标为（　　）
A．（1，0）B．（2，0）C．（0，$\frac{1}{8}$）D．（0，$\frac{1}{16}$）
14．已知函数$f（x）=\frac{1}{3}{x^3}-\frac{1}{2}{x^2}-2x+1$，
（1）求函数f（x）的极值；
（2）若对?x∈[-2，3]，都有s≥f（x）恒成立，求出s的范围．
15．已知$\frac{si{n}^{2}θ+4}{cosθ+1}$=2，则（cosθ+1）（sinθ+1）=（　　）
A．-1B．0C．1D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网