题目内容
已知函数f(x)=lnx+ax2-3x
(Ⅰ)若f′(2)=
,求函数f(x)的单调区间;
(Ⅱ)当a>0时,设函数f(x)的2个极值点为x1,x2,若f(x1)+f(x2)=-
,求a的值.
(Ⅰ)若f′(2)=
| 3 |
| 2 |
(Ⅱ)当a>0时,设函数f(x)的2个极值点为x1,x2,若f(x1)+f(x2)=-
| 9 |
| 4a |
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(Ⅰ)先求导,代入求出a的值,再根据导数和函数的单调性的关系求出单调区间;
(Ⅱ)根据导数等于0,利用韦达定理,得到x1+x2=
,x1•x2=
,由f(x1)+f(x2)=-
,整理化简的ln(2a)=1,求出a的值.
(Ⅱ)根据导数等于0,利用韦达定理,得到x1+x2=
| 3 |
| 2a |
| 1 |
| 2a |
| 9 |
| 4a |
解答:
解:(Ⅰ)∵f(x)=lnx+ax2-3x,
∴函数的定义域为(0,+∞)
∴f′(x)=
+2ax-3,f′(2)=
,
∴
=
+4a-3
解得a=1,
∴f′(x)=
+2x-3=
=
,
令f′(x)=0,解得x=
,或x=1,
当f′(x)>0,即0<x<
,或x>1,
当f′(x)<0,即
<x<1,
故函数的单调增区间为(0,
)∪(1,+∞),单调减区间为(
,1).
(Ⅱ)∵f′(x)=
+2ax-3,函数f(x)的2个极值点为x1,x2,
令f′(x)=0,即
+2ax-3=0,
∴x1,x2是方程的2ax2-3x+1=0两个根,
∴x1+x2=
,x1•x2=
,
∵f(x1)+f(x2)=-
,
∴lnx1+ax12-3x1+lnx2+ax22-3x2=lnx1•x2+a[(x1+x2)2-2x1•x2]-3(x1+x2)=ln
+a(
-
)-
=-
,
即ln(2a)=1,解得a=
∴函数的定义域为(0,+∞)
∴f′(x)=
| 1 |
| x |
| 3 |
| 2 |
∴
| 3 |
| 2 |
| 1 |
| 2 |
解得a=1,
∴f′(x)=
| 1 |
| x |
| 2x2-3x+1 |
| x |
| (2x-1)(x-1) |
| x |
令f′(x)=0,解得x=
| 1 |
| 2 |
当f′(x)>0,即0<x<
| 1 |
| 2 |
当f′(x)<0,即
| 1 |
| 2 |
故函数的单调增区间为(0,
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)∵f′(x)=
| 1 |
| x |
令f′(x)=0,即
| 1 |
| x |
∴x1,x2是方程的2ax2-3x+1=0两个根,
∴x1+x2=
| 3 |
| 2a |
| 1 |
| 2a |
∵f(x1)+f(x2)=-
| 9 |
| 4a |
∴lnx1+ax12-3x1+lnx2+ax22-3x2=lnx1•x2+a[(x1+x2)2-2x1•x2]-3(x1+x2)=ln
| 1 |
| 2a |
| 9 |
| 4a2 |
| 1 |
| a |
| 9 |
| 2a |
| 9 |
| 4a |
即ln(2a)=1,解得a=
| e |
| 2 |
点评:本题主要考查了导数和函数的单调性的关系,以及导数和函数极值点,韦达定理的有关问题,属于中档题

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
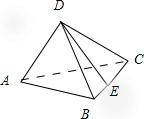 在四面体ABCD中,已知
在四面体ABCD中,已知| AB |
| b |
| AD |
| a |
| AC |
| c |
| BE |
| 1 |
| 2 |
| EC |
| DE |
A、-
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|