题目内容

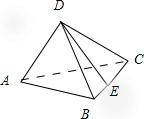在四面体ABCD中，已知
AB
=
b
，
AD
=
a
，
AC
=
c
，
BE
=
1
2
EC
，则
DE
=（　　）
A、-
a
+
2
3
b
+
1
3
c
B、
a
+
2
3
b
+
1
3
c
C、
a
-
2
3
b
+
1
3
c
D、
2
3
a
-
b
+
1
3
c
考点：空间向量的基本定理及其意义
专题：计算题,平面向量及应用
分析：由题意，
DE
=
DB
+
BE
=
AB
-
AD
+
1
3
(
AC
-
AB
)，即可得出结论．
解答： 解：由题意，
DE
=
DB
+
BE
=
AB
-
AD
+
1
3
(
AC
-
AB
)=-
a
+
2
3
b
+
1
3
c
．
故选：A．
点评：本题考查空间向量的线性运算，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
函数f（x）=
log2(1-x)-2a，x≤0
x2-4ax+a，x＞0
有三个不同零点，则实数a的取值范围是（　　）
A、a≤0
B、a＞
1
4
C、
1
4
＜a≤
1
2
或a＜0
D、a＞
1
4
或a＜0
设Γ={（x，y）|x2-y2=1，x＞0}，点M是坐标平面内的动点．若对任意的不同两点P，Q∈Γ，∠PMQ恒为锐角，则点M所在的平面区域（阴影部分）为（　　）
A、
B、
C、
D、
已知双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的右顶点和右焦点分别为A（a，0）、F（c，0），若在直线x=-
a2
c
上存在点P使得∠APF=30°．则该双曲线的离心率的取值范围是（　　）
A、（1，
3+
17
2
]
B、[
3+
17
2
，+∞）
C、（1，4]
D、[4，+∞）
已知直线ax+by=1与圆x2+y2=1相交，则点P（a，b）在（　　）
A、圆上B、圆外
C、圆内D、以上皆有可能
已知函数f（x）=lnx+ax2-3x
（Ⅰ）若f′（2）=
3
2
，求函数f（x）的单调区间；
（Ⅱ）当a＞0时，设函数f（x）的2个极值点为x1，x2，若f（x1）+f（x2）=-
9
4a
，求a的值．
已知f（x）=x2+ax+3-a，当x∈{-2，2}时函数至少有个零点，求a的范围
 
．
已知异面直线a，b均与平面α相交，下列命题：①存在直线m?α，使得m⊥a或m⊥b； ②存在直线m?α，使得m⊥a且m⊥b； ③存在直线m?α，使得m与a和b所成的角相等．其中不正确的命题为
 
．
已知数列{an}的通项公式an=
20
(n+1)2
-1，Sn是数列an的前n项和，S98最接近的整数是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网