题目内容
17.已知正四棱锥的棱长都等于4,则该正四棱锥内切球的表面积为(32-16$\sqrt{3}$)π.分析 求出正四棱锥的体积,然后求出正四棱锥的表面积,利用等体积方法求出内切求的半径,再求表面积.
解答 解:如图所示,设正四棱锥底面的中心为O,则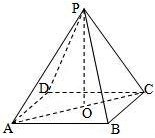
在直角△ABC中,AB=4,AC=4$\sqrt{2}$,
∴AO=CO=2$\sqrt{2}$,
在直角△PAO中,PO=AO=2$\sqrt{2}$,
∴正四棱锥的体积为:$\frac{1}{3}$•42•2$\sqrt{2}$=$\frac{32\sqrt{2}}{3}$;
设正四棱锥内切球的半径为r,
正四棱锥的表面积为:42+4•$\frac{\sqrt{3}}{4}$•42=16+16$\sqrt{3}$,
正四棱锥的体积:$\frac{1}{3}$•(16+16$\sqrt{3}$)•r=$\frac{32\sqrt{2}}{3}$,
∴球的半径r=$\frac{2\sqrt{2}}{1+\sqrt{3}}$=$\sqrt{6}$-$\sqrt{2}$,
∴内切球的表面积为4π•${(\sqrt{6}-\sqrt{2})}^{2}$=(32-16$\sqrt{3}$)π.
故答案为:(32-16$\sqrt{3}$)π.
点评 本题主要考查了正四棱锥内切球的表面积计算问题,等体积法求出球的半径是解题的关键.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
7.已知正三棱柱ABC-A1B1C1的侧棱长与底面边长相等,则AB1与侧面ACC1A1所成角的正弦值等于( )
| A. | $\frac{\sqrt{6}}{4}$ | B. | $\frac{{\sqrt{10}}}{4}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{17}{18}$ |
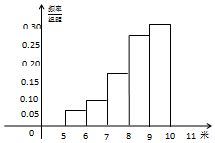 某市为了解今年高中毕业生的身体素质状况,从本市某校高中毕业班中抽取一个班进行实心球测试,成绩在8米及以上的为合格.把所得数据整理后,分成六组得到频率分布直方图的一部分(如图).已知前五个小组的频率分别为0.06.0.10,0.14,0.28,0.30.第六小组的频数是6.
某市为了解今年高中毕业生的身体素质状况,从本市某校高中毕业班中抽取一个班进行实心球测试,成绩在8米及以上的为合格.把所得数据整理后,分成六组得到频率分布直方图的一部分(如图).已知前五个小组的频率分别为0.06.0.10,0.14,0.28,0.30.第六小组的频数是6.