题目内容

x＜0时，函数y=4x+
1
x
（　　）
A、有最小值-4
B、有最大值-4
C、有最小值4
D、有最大值4
考点：基本不等式
专题：不等式的解法及应用
分析：由基本不等式可得-4x+
1
-x
的最值，进而可得原式的最值．
解答： 解：∵x＜0，∴y=4x+
1
x
=-（-4x+
1
-x
），
由基本不等式可得-4x+
1
-x
≥2
(-4x)(-
1
x
)
=4，
当且仅当-4x=
1
-x
，即x=-
1
2
时取等号，
∴y=4x+
1
x
=-（-4x+
1
-x
）≤-4，
故选：B
点评：本题考查基本不等式，注意基本不等式成立的条件是解决问题的关键，属基础题．
练习册系列答案
相关题目
f（x）是定义在区间[-c，c]上的奇函数，其图象如图所示：令g（x）=af（x）+b，则下列关于函数g（x）的叙述正确的是（　　）
A、若a＜0，则函数g（x）的图象关于原点对称．
B、若a=1，0＜b＜2，则方程g（x=0）有大于2的实根．
C、若a=-2，b=0，则函数g（x）的图象关于y轴对称
D、若 a≠0，b=2，则方程g（x）=0有三个实根
函数f（x）=sin（2x+
π
4
），x∈R的最小正周期为（　　）
A、
π
4
B、
π
2
C、π
D、2π
已知角α的终边经过点p0（-3，-4），则cos（
π
2
-α）的值为（　　）
A、-
4
5
B、
3
5
C、
4
5
D、-
3
5
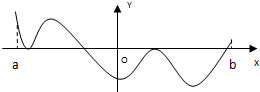函数f（x）的定义域为开区间（a，b），导函数f′（x）在（a，b）内的图象如图所示，则函数f（x）在开区间（a，b）内有极小值点（　　）
A、1个B、2个C、3个D、4个
若曲线f（x）=alnx+bx3+csinx+d；（a，b，c，d均为常数）在x=2014处的切线方程为y+x-2014=0，则f（2014）+f′（2014）=（　　）
A、2013B、2012
C、-1D、0
《爸爸去哪儿》的热播引发了亲子节目的热潮，某节目制作组选取了6户家庭到4个村庄体验农村生活，要求将6户家庭分成4组，其中2组各有2户家庭，另外2组各有1户家庭，则不同的分配方案的总数是（　　）
A、216B、420
C、720D、1080
若复数z=
a+2i
2+i
（a∈R）是纯虚数，则a=（　　）
A、-1B、4C、2D、3
已知函数f（x）=
1
2
ax2-2lnx，a∈R．
（Ⅰ）当a=1时，求曲线y=f（x）在点（1，f（1））处的切线方程；
（Ⅱ）求函数f（x）的单调区间．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网