题目内容
函数f（x）=sin（2x+
），x∈R的最小正周期为（ ）
| π |
| 4 |
A、
| ||
B、
| ||
| C、π | ||
| D、2π |
考点：三角函数的周期性及其求法
专题：三角函数的图像与性质
分析：由条件利用利y=Asin（ωx+φ）的周期等于 T=
，可得结论．
| 2π |
| ω |
解答：
解：函数f（x）=sin（2x+
），x∈R的最小正周期为T=
=π，
故选：C．
| π |
| 4 |
| 2π |
| 2 |
故选：C．
点评：本题主要考查三角函数的周期性及其求法，利用了y=Asin（ωx+φ）的周期等于 T=
，属于基础题．
| 2π |
| ω |
练习册系列答案
优生乐园系列答案
新编小学单元自测题系列答案
相关题目
一个几何体的三视图如图所示，其俯视图为正三角形，则这个几何体的体积为（ ）
A、12
| ||
B、36
| ||
C、27
| ||
| D、6 |
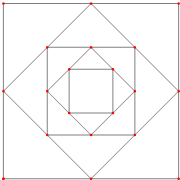如图，画一个边长为10cm的正方形，再将这个正方形各边的中点相连得到第二个正方形，依此类推，这样一共画了五个正方形，则它们的面积的和为（ ）| A、193.75cm2 |
| B、387.5cm2 |
| C、187.5cm2 |
| D、200.75cm2 |
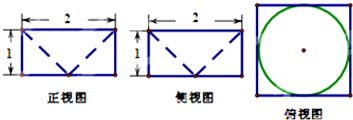
如图是一个空间几何体的三视图，则该几何体的体积为（ ）
A、4-
| ||
B、8-
| ||
C、4-
| ||
D、8-
|
如图的程序框图，如输入x=2，则输出y为（ ）
| A、0 | B、-1 | C、-2 | D、-3 |
x＜0时，函数y=4x+
（ ）
| 1 |
| x |
| A、有最小值-4 |
| B、有最大值-4 |
| C、有最小值4 |
| D、有最大值4 |
若函数f（x）=ax+cos2x在区间[0，
]上是单调函数，则实数a的取值范围是（ ）
| π |
| 6 |
A、a≤0或a≥
| ||
B、a≥
| ||
C、a≥0或a≤-
| ||
D、a≤-
|