题目内容
 f(x)是定义在区间[-c,c]上的奇函数,其图象如图所示:令g(x)=af(x)+b,则下列关于函数g(x)的叙述正确的是( )
f(x)是定义在区间[-c,c]上的奇函数,其图象如图所示:令g(x)=af(x)+b,则下列关于函数g(x)的叙述正确的是( )| A、若a<0,则函数g(x)的图象关于原点对称. |
| B、若a=1,0<b<2,则方程g(x=0)有大于2的实根. |
| C、若a=-2,b=0,则函数g(x)的图象关于y轴对称 |
| D、若 a≠0,b=2,则方程g(x)=0有三个实根 |
考点:利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:当a<0,b≠0时,由g(0)=af(0)+b=b≠0可排除A;方程g(x)=0,其实根即y=f(x)的图象与直线y=-b的交点的横坐标.由图象可判断B正确.
解答:
解:当a<0,b≠0时,g(0)=af(0)+b=b≠0,
∴g(x)不是奇函数,此时函数g(x)的图象不关于原点对称,故A不正确.
方程g(x)=0,即af(x)+b=0,当a≠0时,其实根即y=f(x)的图象与直线y=-b的交点的横坐标.
当a=1,0<b<2时,-b∈(-2,0),由图所知,y=f(x)的图象与直线y=-b有一交点的横坐标大于2,故B正确.
故选B.
∴g(x)不是奇函数,此时函数g(x)的图象不关于原点对称,故A不正确.
方程g(x)=0,即af(x)+b=0,当a≠0时,其实根即y=f(x)的图象与直线y=-b的交点的横坐标.
当a=1,0<b<2时,-b∈(-2,0),由图所知,y=f(x)的图象与直线y=-b有一交点的横坐标大于2,故B正确.
故选B.
点评:该题考查利用导数研究函数的单调性、极值,考查数形结合思想,属中档题.

练习册系列答案
相关题目
10盏路灯,为节约用电,关掉其中三盏,不关两端,不连续关灯,(任两盏不连续).则共有( )种方法.
| A、15 | B、20 | C、36 | D、49 |
函数在y=
定义域内( )
| 4x |
| x2+1 |
| A、有最大值2,无最小值 |
| B、无最大值,有最小值-2 |
| C、有最大值2,最小值-2 |
| D、无最值 |
一个几何体的三视图如图所示,其俯视图为正三角形,则这个几何体的体积为( )


A、12
| ||
B、36
| ||
C、27
| ||
| D、6 |
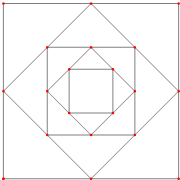 如图,画一个边长为10cm的正方形,再将这个正方形各边的中点相连得到第二个正方形,依此类推,这样一共画了五个正方形,则它们的面积的和为( )
如图,画一个边长为10cm的正方形,再将这个正方形各边的中点相连得到第二个正方形,依此类推,这样一共画了五个正方形,则它们的面积的和为( )| A、193.75cm2 |
| B、387.5cm2 |
| C、187.5cm2 |
| D、200.75cm2 |
x<0时,函数y=4x+
( )
| 1 |
| x |
| A、有最小值-4 |
| B、有最大值-4 |
| C、有最小值4 |
| D、有最大值4 |