题目内容
若复数z=
（a∈R）是纯虚数，则a=（ ）
| a+2i |
| 2+i |
| A、-1 | B、4 | C、2 | D、3 |
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：由条件利用，两个复数代数形式的乘除法法则化简可得z=
是纯虚数，可得2a+2=0，且 4-a≠0，由此求得a的值．
| 2a+2+(4-a)i |
| 5 |
解答：
解：∵复数z=
=
=
是纯虚数，
∴2a+2=0，且 4-a≠0，
解得 a=-1，
故选：A．
| a+2i |
| 2+i |
| (a+2i)(2-i) |
| (2+i)(2-i) |
| 2a+2+(4-a)i |
| 5 |
∴2a+2=0，且 4-a≠0，
解得 a=-1，
故选：A．
点评：本题主要考查复数的基本概念，两个复数代数形式的乘除法法则的应用，虚数单位i的幂运算性质，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
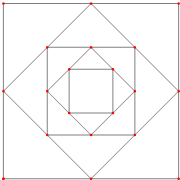如图，画一个边长为10cm的正方形，再将这个正方形各边的中点相连得到第二个正方形，依此类推，这样一共画了五个正方形，则它们的面积的和为（ ）| A、193.75cm2 |
| B、387.5cm2 |
| C、187.5cm2 |
| D、200.75cm2 |
x＜0时，函数y=4x+
（ ）
| 1 |
| x |
| A、有最小值-4 |
| B、有最大值-4 |
| C、有最小值4 |
| D、有最大值4 |
若用C、R和I分别表示复数集、实数集和纯虚数集，其中C为全集，那么有（ ）
| A、C=R∪I |
| B、R∪∁CI=R |
| C、∁CR=C∩I |
| D、∁CR∩I=I |
下列命题不正确的是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知函数f（x）=
，若存在实数t使得f（x）在R上为单调函数，则a的取值范围是（ ）
|
| A、a≥0 | B、a＜0 |
| C、a≤t | D、a＜-t |
若函数f（x）=ax+cos2x在区间[0，
]上是单调函数，则实数a的取值范围是（ ）
| π |
| 6 |
A、a≤0或a≥
| ||
B、a≥
| ||
C、a≥0或a≤-
| ||
D、a≤-
|