题目内容
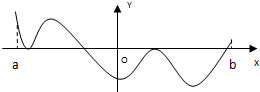函数f（x）的定义域为开区间（a，b），导函数f′（x）在（a，b）内的图象如图所示，则函数f（x）在开区间（a，b）内有极小值点（ ）| A、1个 | B、2个 | C、3个 | D、4个 |
考点：利用导数研究函数的极值
专题：导数的概念及应用
分析：由图象得：导函数f′（x）=0有3个根，只有在b附近的根满足根的左边为负值，根的右边为正值，故函数只有1个极小值点．从而问题得解．
解答：
解：由图象得：导函数f′（x）=0有3个根，
只有在b附近的根满足根的左边为负值，根的右边为正值，
故函数只有1个极小值点，
故选：A．
只有在b附近的根满足根的左边为负值，根的右边为正值，
故函数只有1个极小值点，
故选：A．
点评：本题考察了函数的极值问题，导数的应用，是一道基础题．
练习册系列答案
步步高达标卷系列答案
相关题目
10盏路灯，为节约用电，关掉其中三盏，不关两端，不连续关灯，（任两盏不连续）．则共有（ ）种方法．
| A、15 | B、20 | C、36 | D、49 |
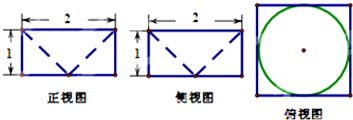
如图是一个空间几何体的三视图，则该几何体的体积为（ ）
A、4-
| ||
B、8-
| ||
C、4-
| ||
D、8-
|
如图的程序框图，如输入x=2，则输出y为（ ）
| A、0 | B、-1 | C、-2 | D、-3 |
为大力提倡“厉行节约，反对浪费”，某市通过随机询问100名性别不同的居民是否能做到“光盘”行动，得到如下的列联表：
下面的临界值供参考：
x2=
，其中n*1=n11+n22，n*2=n12+n21，n1*=n11+n12，n2*=n21+n22，n=n11+n22+n12+n21
下列结论正确的是（ ）
| 做不到“光盘” | 能做到“光盘” | 合计 | |
| 男 | 45 | 10 | 55 |
| 女 | 25 | 20 | 45 |
| 合计 | 70 | 30 | 100 |
x2=
| n(n11n22n12n21)2 |
| n1*n2*n*1n*2 |
| P（x2≥k） | 0.05 | 0.010 | 0.005 | 0.001 |
| K | 3.841 | 6.635 | 7.879 | 10.828 |
| A、有95%以上的把握认为“该市居民能否做到“光盘”与性别有关 |
| B、有99%以上的把握认为“该市居民能否做到“光盘”与性别有关 |
| C、有99.5%以上的把握认为“该市居民能否做到“光盘”与性别有关 |
| D、性别不同决定了能否做到“光盘” |
x＜0时，函数y=4x+
（ ）
| 1 |
| x |
| A、有最小值-4 |
| B、有最大值-4 |
| C、有最小值4 |
| D、有最大值4 |
设函数f（x）的导函数为f′（x），对任意x∈R都有0＜f′（x）＜2成立，则（ ）
| A、f（1）＜f（3）＜f（2）+2 |
| B、f（2）+2＜f（3）＜f（1） |
| C、f（1）＜f（2）+2＜f（3） |
| D、f（2）+2＜f（1）＜f（3） |
下列命题不正确的是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
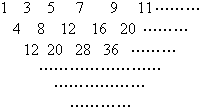如图的倒三角形数阵满足：①第一行的第n 个数，分别是1，3，5，7，9，…，2n-1； ②从第二行起，各行中的每一个数都等于它肩上的两数之和； ③数阵共有n行；