题目内容
已知函数f(x)=-x3+1,
(1)求f(x)的单调减区间;
(2)求f(x)过点(-2,1)的切线方程.
(1)求f(x)的单调减区间;
(2)求f(x)过点(-2,1)的切线方程.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的概念及应用
分析:(1)求出函数的导数,从而求出函数的单调区间;(2)先求出切点坐标,从而求出切线方程.
解答:
解:(1)∵f′(x)=-3x2≤0,
∴函数f(x)在(-∞,+∞)递减;
(2)设切点A(x0,y0),
f′(x0)=-3x02=k,y0=-x03+1,y0-1=k(x0+2),
以上三式联立解得:x0=3或x0=0,y0=-26或y0=1,
∴切线方程为:y=-27x+55或y=1.
∴函数f(x)在(-∞,+∞)递减;
(2)设切点A(x0,y0),
f′(x0)=-3x02=k,y0=-x03+1,y0-1=k(x0+2),
以上三式联立解得:x0=3或x0=0,y0=-26或y0=1,
∴切线方程为:y=-27x+55或y=1.
点评:本题考查了函数的单调性,求曲线的切线方程问题,找到切点是解决本题的关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
随机投掷1枚骰子,掷出的点数恰好是3的倍数的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,
如图,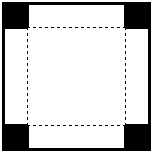 如图,一边长为48cm的正方形铁皮,在它的四角上切去相等的小正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
如图,一边长为48cm的正方形铁皮,在它的四角上切去相等的小正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?