Question

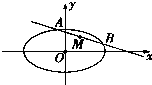如图，

x2

16

+

y2

4

=1内一点M（1，1）的弦AB，若点M恰为弦AB的中点，求直线AB的方程．

Answer 1

考点：椭圆的简单性质

专题：圆锥曲线的定义、性质与方程

分析：首先，设出直线AB的方程，然后，联立方程组，消去Y，结合根与系数的关系，利用中点关系建立等式，求解直线的斜率即可得到结果．

解答： 解：设直线AB的斜率为k，则
其方程为：y-1=k（x-1），
联立方程组

y=k(x-1)+1 x2 16 + y2 4 =1

，
消去y，并整理，得
（1+4k²）x²+8k（1-k）x+4（1-k）²-16=0，
设A（x₁，y₁），B（x₂，y₂），则
x₁+x₂=

8k(k-1)

1+4k2

，
∵M（1，1）为弦AB的中点，
∴

8k(k-1)

1+4k2

=2，
解得，k=-

1

4

，
∴直线AB的方程为：y-1=-

1

4

（x-1），
化简，得
x+4y-5=0．
∴直线AB的方程x+4y-5=0．

点评：本题重点考查了直线与椭圆的位置关系、直线的方程等知识，本题涉及到弦中点问题，注意弦中点问题的处理思路和方法．