题目内容
证明:两个等差数列的相同的项按原来的前后次序组成一个等差数列,且公差为原来两个公差的最小公倍数.
考点:等差关系的确定
专题:等差数列与等比数列
分析:分别设出两个等差数列,求出它们共同的第n项和第n+1项,两项作差后说明当两项的差为原两等差数列公差的最小公倍数时为常数,符合等差数列的概念,从而说明两个等差数列的相同的项按原来的前后次序组成一个等差数列,且公差为原来两个公差的最小公倍数.
解答:
证明:设两个等差数列分别为{an},{bn},
首项分别为a1,b1,公差分别为d1,d2,
再设其第n个相同的项为cn,
则cn=ai=a1+(i-1)d1,cn=bj=b1+(j-1)d2,
再设其第n+1个相同的项为cn+1,
则cn+1=ak=a1+(k-1)d1=cn+(k-i)d1,
cn+1=bm=b1+(m-1)d2=cn+(m-j)d2,
即cn+1-cn=(k-i)d1=(m-j)d2,
令k-i=z1,m-j=z2(z1,z2∈N*),
则z1d1=z2d2,
∴当z1d2为d1,d2的最小公倍数时,能够两个等差数列的相同的项按原来的前后次序组成一个等差数列,且公差为原来两个公差的最小公倍数.
首项分别为a1,b1,公差分别为d1,d2,
再设其第n个相同的项为cn,
则cn=ai=a1+(i-1)d1,cn=bj=b1+(j-1)d2,
再设其第n+1个相同的项为cn+1,
则cn+1=ak=a1+(k-1)d1=cn+(k-i)d1,
cn+1=bm=b1+(m-1)d2=cn+(m-j)d2,
即cn+1-cn=(k-i)d1=(m-j)d2,
令k-i=z1,m-j=z2(z1,z2∈N*),
则z1d1=z2d2,
∴当z1d2为d1,d2的最小公倍数时,能够两个等差数列的相同的项按原来的前后次序组成一个等差数列,且公差为原来两个公差的最小公倍数.
点评:本题考查了等差关系的确定,关键是对题意的理解与应用,考查了学生综合分析问题和解决问题的能力,属难度较大的题目.

练习册系列答案
相关题目
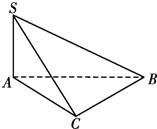 如图,SA⊥面ABC,∠ACB=90°,∠ABC=30°,AC=1,SB=2
如图,SA⊥面ABC,∠ACB=90°,∠ABC=30°,AC=1,SB=2