题目内容
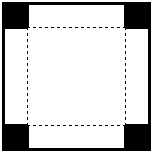如图，一边长为48cm的正方形铁皮，在它的四角上切去相等的小正方形，再把它的边沿虚线折起，做成一个无盖的方底箱子，箱底的边长是多少时，箱子的容积最大？最大容积是多少？考点：基本不等式在最值问题中的应用
专题：计算题,应用题,函数的性质及应用,导数的概念及应用
分析：设箱底边长为xcm，结合题意可得容积V（x）=
（48x2-x3）（0＜x＜48）．再用导数工具研究V（x）在区间（0，48）上的单调性，可知当x=40时V（x）达到最大值．由此得到本题答案．
| 1 |
| 2 |
解答：
解：设箱底边长为xcm，则箱高h=
，
∴箱子容积V（x）=x2h=
（48x2-x3）（0＜x＜48）．
求导数，得V′（x）=48x-
x2，
令V′（x）=0，解得x=0（不合题意，舍去），x=32，
∵x∈（0，32）时，V′（x）＞0；x∈（32，48）时，V′（x）＜0，
∴V（x）在区间（0，32）上为增函数，区间（32，48）上为减函数，
由此可得V（x）的最大值是V（32）=8192．
故箱底的边长是32cm时，箱子的容积最大，最大容积是8192cm3．
| 48-x |
| 2 |
∴箱子容积V（x）=x2h=
| 1 |
| 2 |
求导数，得V′（x）=48x-
| 3 |
| 2 |
令V′（x）=0，解得x=0（不合题意，舍去），x=32，
∵x∈（0，32）时，V′（x）＞0；x∈（32，48）时，V′（x）＜0，
∴V（x）在区间（0，32）上为增函数，区间（32，48）上为减函数，
由此可得V（x）的最大值是V（32）=8192．
故箱底的边长是32cm时，箱子的容积最大，最大容积是8192cm3．
点评：本题以一个实际问题为例，求铁箱的容积最大值．着重考查了函数模型及其应用和利用导数研究函数的单调性、求最值等知识，属于中档题．
练习册系列答案
相关题目
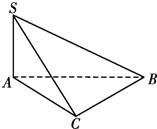如图，SA⊥面ABC，∠ACB=90°，∠ABC=30°，AC=1，SB=2