题目内容

函数f（x）=
3
x-2
+4，定义域x∈（1，2）∪（2，3），求函数f（x）的值域．
考点：函数的值域
专题：计算题,函数的性质及应用
分析：由x的取值范围先确定
3
x-2
的取值范围，进而求函数f（x）的值域．
解答： 解：①∵1＜x＜2，
∴-1＜x-2＜0，
∴
3
x-2
＜-3；
②∵2＜x＜3，
∴0＜x-2＜1；
∴
3
x-2
＞3；
∴
3
x-2
+4＜1或
3
x-2
+4＞7；
即函数f（x）的值域为（-∞，1）∪（7，+∞）．
点评：本题考查了函数的值域的求法，注意定义域分段时要讨论，属于基础题．
练习册系列答案
相关题目
已知向量
a
=（cosα，sinα），
b
=（cosβ，sinβ），且
a
，
b
满足关系|k
a
+
b
|=
3
|
a
-k
b
|，（k为正实数）．
（1）求将
a
•
b
表示为k的函数f（k）；
（2）求函数f（k）的最小值及取最小值时
a
 ， 
b
的夹角θ．
某种产品的广告费支出x与销售额y（单位：百万元）之间有如下对应数据：
x24568
y3040605070
（Ⅰ）画出散点图；
（Ⅱ）求回归直线方程；
（Ⅲ）试预测广告费支出为10百万元时，销售额多大？
（可能用到的公式：
b
=
n
i=1
xiyi-n
.
xy
n
i=1
xi2-n
.
x
2
，
a
=
.
y
-
b
.
x
，其中
?
a
、
?
b
是对回归直线方程
y
=a+bx中系数a、b按最小二乘法求得的估计值）
已知命题p：|x2-6|≥6，q：x∈z，且“p∧q”与“?q”同时为假命题，求x的值．
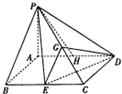已知在四棱锥P-ABCD中，底面ABCD是平行四边形，PA⊥平面ABCD，PA=
3
，AB=1，AD=2，∠BAD=120°，E，G，H分别是BC，PC，AD的中点．
（Ⅰ）求证：PH∥平面GED；
（Ⅱ）求证：平面PAE⊥平面PDE；
（Ⅲ）求三棱锥P-GED的体积．
（Ⅰ）已知log189=a，18b=5，试用a、b表示log1845的值；
（Ⅱ）已知log147=a，log145=b，用a、b表示log3528．
计算：（1）
3(-4)3
-(
1
2
)0+0.25
1
2
×(
2
)4
（2）lg4+lg25+4-
1
2
-（4-π）0．
已知函数f（x）=
x-2
-
x+2
，判断f（x）的奇偶性．
在平面直角坐标系xOy中过定点Q（1，1）的直线l与曲线C：y=
x
x-1
交与M，N点，则
ON
•
OQ
-
MO
•
OQ
=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网