题目内容
已知命题p：|x2-6|≥6，q：x∈z，且“p∧q”与“?q”同时为假命题，求x的值．
考点：复合命题的真假
专题：简易逻辑
分析：首先，根据“p∧q”与“?q”同时为假命题，对命题p分为假命题和真命题两种情形进行求解．
解答：
解：∵“p∧q”与“?q”同时为假命题，
∴p为假命题q为真命题，
当P为真命题时：
根据x2-6≥6或x2-6≤-6 解得
x≥2
或x≤-2
或x=0
∴当p为假命题时：
-2
＜x＜0或0＜x＜2
且q为真命题，
因此x的值为-3，-2，-1，1，2，3．
∴p为假命题q为真命题，
当P为真命题时：
根据x2-6≥6或x2-6≤-6 解得
x≥2
| 3 |
| 3 |
∴当p为假命题时：
-2
| 3 |
| 3 |
且q为真命题，
因此x的值为-3，-2，-1，1，2，3．
点评：本题重点考查了常用逻辑用语、复合命题的真假判断等知识，属于中档题．
练习册系列答案
相关题目
如图所示，|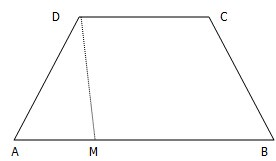
如图所示的四边形ABCD为等腰梯形，两腰与底边的夹角为45°，上底边长为2，高为2．点M从A点出发，沿梯形的边AB，BC运动，最后到达点C，若x表示点M的移动路程，S表示线段DM在四边形ABCD内部扫过的面积．
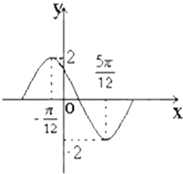函数y=Asin（ωx+ϕ）（其中A＞0，ω＞0，0＜ϕ＜π）在一个周期内的图象如下