题目内容
在平面直角坐标系x0y中,直线
(t为参数)与圆
(θ为参数)相切,切点在第一象限,则实数a的值为 .
|
|
考点:参数方程化成普通方程
专题:直线与圆,坐标系和参数方程
分析:把直线和圆的参数方程都化为普通方程,由直线与圆相切d=r,切点在第一象限,求出a的值.
解答:
解:圆的参数方程
(θ为参数)
化为普通方程是(x-1)2+y2=1,
直线的参数方程
(t为参数)
化为普通方程是x+y=a;
直线与圆相切,则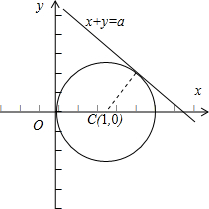
圆心C(1,0)到直线的距离是d=r,
即
=1;
解得|1-a|=
,
∴a=
+1,或a=1-
;
∵切点在第一象限,∴a=
+1;
故答案为:
+1.
|
化为普通方程是(x-1)2+y2=1,
直线的参数方程
|
化为普通方程是x+y=a;
直线与圆相切,则

圆心C(1,0)到直线的距离是d=r,
即
| |1+0-a| | ||
|
解得|1-a|=
| 2 |
∴a=
| 2 |
| 2 |
∵切点在第一象限,∴a=
| 2 |
故答案为:
| 2 |
点评:本题考查了参数方程的应用问题,解题时先把参数方程化为普通方程,再利用直线与圆的位置关系进行解答,是基础题.

练习册系列答案
相关题目