题目内容
已知函数f(x)在R上单调递增,?a,b∈R满足a+b>0,则f(a)+f(b) f(-a)+f(-b)(用“>”,“=”或“<”填空)
考点:函数单调性的性质
专题:函数的性质及应用
分析:由题意可得 a>-b,b>-a,再根据增函数的定义可得f(a)>f(-b),f(b)>f(-a),可得f(a)+f(b)>f(-a)+f(-b).
解答:
解:∵函数f(x)在R上单调递增,?a,b∈R满足a+b>0,∴a>-b,b>-a,
∴f(a)>f(-b),f(b)>f(-a),∴f(a)+f(b)>f(-a)+f(-b),
故答案为:>.
∴f(a)>f(-b),f(b)>f(-a),∴f(a)+f(b)>f(-a)+f(-b),
故答案为:>.
点评:本题主要考查增函数的定义,不等式的基本性质应用,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验.根据收集到的数据(如下表),由最小二乘法求得回归方程
=0.74x+50
则m+n的值为( )
 |
| y |
| 零件数x(个) | 10 | 20 | 30 | 40 | 50 |
| 加工时间y(min) | 62 | m | n | 81 | 89 |
| A、137 | B、129 |
| C、121 | D、118 |
已知数列{an}的通项公式an=2014sin
,则a1+a2+…+a2014=( )
| nπ |
| 2 |
| A、2012 | B、2013 |
| C、2014 | D、2015 |
若正数a,b满足
+
=1,则
+
的最小值为( )
| 1 |
| a |
| 1 |
| b |
| 4 |
| a-1 |
| 16 |
| b-1 |
| A、16 | B、25 | C、36 | D、49 |
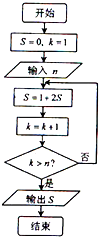 阅读如图所示的程序框图,运行相应的程序,如果输入某个正整数n后,输出的S∈(30,40),那么n的值为( )
阅读如图所示的程序框图,运行相应的程序,如果输入某个正整数n后,输出的S∈(30,40),那么n的值为( )